25. (12分)如图,B是线段AD上一动点,沿$A→D→A$以2个单位长度每秒的速度往返运动1次,C是线段BD的中点,$AD= 10$,记点B运动时间为t s($0\leqslant t\leqslant 10$).
(1) 当$t= 2$时,①$AB=$
(2) ① 点B沿点A向点D运动时,$AB=$
(3) 在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
解:(1)②BD=AD-AB=6
∵C是BD中点,∴$CD=\frac {1}{2}BD=3$
(3)EC长不变
∵E是AB中点,∴AE=BE
∴$EC=EB+BC=\frac {1}{2}AB+\frac {1}{2}BD=\frac {1}{2}AD=5$

(1) 当$t= 2$时,①$AB=$
4
;②求线段CD的长度.(2) ① 点B沿点A向点D运动时,$AB=$
2t
;② 点B沿点D向点A运动时,$AB=$(20-2t)
.(用含t的代数式表示)(3) 在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
解:(1)②BD=AD-AB=6
∵C是BD中点,∴$CD=\frac {1}{2}BD=3$
(3)EC长不变
∵E是AB中点,∴AE=BE
∴$EC=EB+BC=\frac {1}{2}AB+\frac {1}{2}BD=\frac {1}{2}AD=5$
答案:4
2t
(20-2t)
解:(1)②BD=AD-AB=6
∵C是BD中点,∴$CD=\frac {1}{2}BD=3$
(3)EC长不变
∵E是AB中点,∴AE=BE
∴$EC=EB+BC=\frac {1}{2}AB+\frac {1}{2}BD=\frac {1}{2}AD=5$
2t
(20-2t)
解:(1)②BD=AD-AB=6
∵C是BD中点,∴$CD=\frac {1}{2}BD=3$
(3)EC长不变
∵E是AB中点,∴AE=BE
∴$EC=EB+BC=\frac {1}{2}AB+\frac {1}{2}BD=\frac {1}{2}AD=5$
26. (12分)如图①,数轴上点A表示的数为-2,点B表示的数为6,点P从点A出发以1个单位长度每秒的速度沿数轴向右匀速运动,点Q从点B出发以3个单位长度每秒的速度沿数轴向左匀速运动,点M,N分别为PA,QB的中点.点P,Q同时出发,当点P到达点B时,运动停止,设点P,Q运动时间为t s.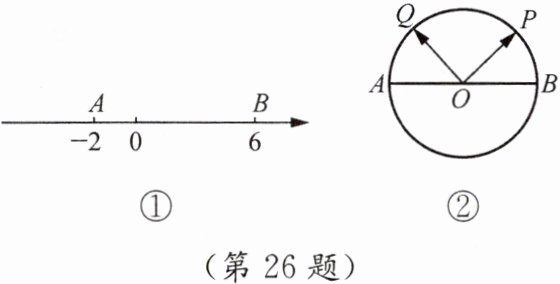
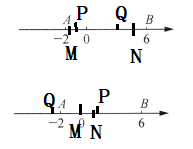
(1) 当点P,Q相遇时,$t= $______,$MN= $______.
(2) 当PQ之间的距离为4个单位长度时,求线段MN的长.
(3) 学校数学社团的学生自制了一个圆形转盘,如图②,O为转盘圆心,点A,O,B在一条直线上,指针OP从OA出发绕点O按顺时针方向转动,指针OQ也以相同的速度从OB出发绕点O按逆时针方向转动.OP,OQ同时出发,当OP,OQ分别到达OB,OA时,运动停止.已知OM平分$\angle AOP$,ON平分$\angle BOQ$,设$\angle MON= \alpha$,$\angle POQ= \beta$.试探索α与β的关系.(直接写出答案)

(1) 当点P,Q相遇时,$t= $______,$MN= $______.
(2) 当PQ之间的距离为4个单位长度时,求线段MN的长.
(3) 学校数学社团的学生自制了一个圆形转盘,如图②,O为转盘圆心,点A,O,B在一条直线上,指针OP从OA出发绕点O按顺时针方向转动,指针OQ也以相同的速度从OB出发绕点O按逆时针方向转动.OP,OQ同时出发,当OP,OQ分别到达OB,OA时,运动停止.已知OM平分$\angle AOP$,ON平分$\angle BOQ$,设$\angle MON= \alpha$,$\angle POQ= \beta$.试探索α与β的关系.(直接写出答案)
答案:
2
4
解:(2)P表示数为-2+t,Q表示数为6-3t
由题,|-2+t-6+3t|=4,解得t=1或3
t=1时$,MN=MP+PQ+QN=\frac {1}{2}(-2+t+2)+4+\frac {1}{2}(6-6+3t)=4+2t=6$
t=3时,MN=QP-QM-PN=QP-QN+MN-PM+MN=2MN+4-2t,则MN=2t-4=2
综上,MN=2或6
(3)2α+β=180°或2α-β=180°
2
4
解:(2)P表示数为-2+t,Q表示数为6-3t
由题,|-2+t-6+3t|=4,解得t=1或3
t=1时$,MN=MP+PQ+QN=\frac {1}{2}(-2+t+2)+4+\frac {1}{2}(6-6+3t)=4+2t=6$
t=3时,MN=QP-QM-PN=QP-QN+MN-PM+MN=2MN+4-2t,则MN=2t-4=2
综上,MN=2或6
(3)2α+β=180°或2α-β=180°

解析:
26. (1)
当点P,Q相遇时,根据路程和等于AB距离:
$1 \cdot t + 3 \cdot t = 6 - (-2)$
$4t = 8$,解得$t=2$。
此时,点P表示的数:$-2 + 1 × 2 = 0$;点Q表示的数:$6 - 3 × 2 = 0$。
M为PA中点:$M = \frac{-2 + 0}{2} = -1$;
N为QB中点:$N = \frac{0 + 6}{2} = 3$;
$MN = 3 - (-1) = 4$。
故答案为:2;4。
(2)
PQ距离为4时,$|(-2 + t) - (6 - 3t)| = 4$,即$|4t - 8| = 4$。
解得$t=1$或$t=3$。
当$t=1$时:
$M = \frac{-2 + (-2 + 1)}{2} = \frac{-3}{2} = -1.5$,
$N = \frac{(6 - 3 × 1) + 6}{2} = \frac{9}{2} = 4.5$,
$MN = 4.5 - (-1.5) = 6$。
当$t=3$时:
$M = \frac{-2 + (-2 + 3)}{2} = \frac{-1}{2} = -0.5$,
$N = \frac{(6 - 3 × 3) + 6}{2} = \frac{3}{2} = 1.5$,
$MN = 1.5 - (-0.5) = 2$。
故线段MN的长为6或2。
(3)
设运动时间为$t$,速度为$v$,则$\angle AOP = vt$,$\angle BOQ = vt$。
$\beta = \angle POQ = 180^\circ - 2vt$,
$\angle AOM = \frac{vt}{2}$,$\angle BON = \frac{vt}{2}$,
$\alpha = \angle MON = 180^\circ - \frac{vt}{2} - \frac{vt}{2} = 180^\circ - vt$。
联立得$\alpha = \frac{\beta + 180^\circ}{2}$,即$2\alpha - \beta = 180^\circ$。
故答案为:$2\alpha - \beta = 180^\circ$。
当点P,Q相遇时,根据路程和等于AB距离:
$1 \cdot t + 3 \cdot t = 6 - (-2)$
$4t = 8$,解得$t=2$。
此时,点P表示的数:$-2 + 1 × 2 = 0$;点Q表示的数:$6 - 3 × 2 = 0$。
M为PA中点:$M = \frac{-2 + 0}{2} = -1$;
N为QB中点:$N = \frac{0 + 6}{2} = 3$;
$MN = 3 - (-1) = 4$。
故答案为:2;4。
(2)
PQ距离为4时,$|(-2 + t) - (6 - 3t)| = 4$,即$|4t - 8| = 4$。
解得$t=1$或$t=3$。
当$t=1$时:
$M = \frac{-2 + (-2 + 1)}{2} = \frac{-3}{2} = -1.5$,
$N = \frac{(6 - 3 × 1) + 6}{2} = \frac{9}{2} = 4.5$,
$MN = 4.5 - (-1.5) = 6$。
当$t=3$时:
$M = \frac{-2 + (-2 + 3)}{2} = \frac{-1}{2} = -0.5$,
$N = \frac{(6 - 3 × 3) + 6}{2} = \frac{3}{2} = 1.5$,
$MN = 1.5 - (-0.5) = 2$。
故线段MN的长为6或2。
(3)
设运动时间为$t$,速度为$v$,则$\angle AOP = vt$,$\angle BOQ = vt$。
$\beta = \angle POQ = 180^\circ - 2vt$,
$\angle AOM = \frac{vt}{2}$,$\angle BON = \frac{vt}{2}$,
$\alpha = \angle MON = 180^\circ - \frac{vt}{2} - \frac{vt}{2} = 180^\circ - vt$。
联立得$\alpha = \frac{\beta + 180^\circ}{2}$,即$2\alpha - \beta = 180^\circ$。
故答案为:$2\alpha - \beta = 180^\circ$。