2. 用代数式表示“a与b的平方的和”为 (
A.$(a+b)^2$
B.$a+b^2$
C.$a^2+b$
D.$a^2+b^2$
B
)A.$(a+b)^2$
B.$a+b^2$
C.$a^2+b$
D.$a^2+b^2$
答案:B
解析:
“a与b的平方的和”表示先计算b的平方,再与a相加,即$a + b^2$。
3. 用代数式表示下列数量,不恰当的有
① 长为a、宽为$1\frac{1}{2}的长方形面积记为1\frac{1}{2}a$;
② 长、宽、高分别为2,x,y的长方体体积记为$2×x×y$;
③ 苹果a元/kg,买3b kg苹果需要a3b元;
④ 儿子的年龄是x岁,父亲的年龄是儿子的2倍多3岁,父亲年龄为(2x+3)岁.
①②③
(填序号).① 长为a、宽为$1\frac{1}{2}的长方形面积记为1\frac{1}{2}a$;
② 长、宽、高分别为2,x,y的长方体体积记为$2×x×y$;
③ 苹果a元/kg,买3b kg苹果需要a3b元;
④ 儿子的年龄是x岁,父亲的年龄是儿子的2倍多3岁,父亲年龄为(2x+3)岁.
答案:①②③
①代数式中有字母时不能使用带分数,会造成歧义
②字母相乘的最终结果省略乘号
③数字写在字母前面
①代数式中有字母时不能使用带分数,会造成歧义
②字母相乘的最终结果省略乘号
③数字写在字母前面
4. 在甲商店累计购物超过200元后,超出200元的部分按八五折收费;在乙商店累计购物超过100元后,超出100元的部分按九折收费.现某顾客累计购物x元(x>200),若在甲商店购物,则实际支付
0.85x+30
元;若在乙商店购物,则实际支付0.9x+10
元.(均用含x的代数式表示)答案:(0.85x+30)
(0.9x+10)
(0.9x+10)
解析:
在甲商店购物:$200 + 0.85(x - 200) = 0.85x + 30$
在乙商店购物:$100 + 0.9(x - 100) = 0.9x + 10$
$0.85x + 30$;$0.9x + 10$
在乙商店购物:$100 + 0.9(x - 100) = 0.9x + 10$
$0.85x + 30$;$0.9x + 10$
1. 填空题:
(1)“x的5倍与y的和的一半”可以表示为
(2)“与m-3的积是5的数”可以表示为
(3)甲、乙两车分别以v km/h和u km/h的速度同时从A,B两地相向而行,3 h后两车相遇,则A,B两地相距
(4)电影院第一排有m个座位,若每一排都比前一排多1个座位,则第n排的座位数是
(1)“x的5倍与y的和的一半”可以表示为
$\frac{1}{2}(5x+y)$
;(2)“与m-3的积是5的数”可以表示为
$\frac{5}{m-3}$
;(3)甲、乙两车分别以v km/h和u km/h的速度同时从A,B两地相向而行,3 h后两车相遇,则A,B两地相距
(3v+3u)
km;(4)电影院第一排有m个座位,若每一排都比前一排多1个座位,则第n排的座位数是
m+n-1
.答案:$\frac{1}{2}(5x+y)$
$\frac{5}{m-3}$
(3v+3u)
m+n-1
$\frac{5}{m-3}$
(3v+3u)
m+n-1
解析:
(1) x的5倍为5x,与y的和为5x+y,一半即(5x+y)÷2,可表示为$\frac{5x+y}{2}$;
(2) 设该数为x,由题意得x(m-3)=5,解得x=$\frac{5}{m-3}$;
(3) 甲3小时行驶3v km,乙3小时行驶3u km,两地距离为3v+3u=3(v+u) km;
(4) 第1排m个,第2排m+1个,第3排m+2个,...,第n排m+(n-1)=m+n-1个。
(2) 设该数为x,由题意得x(m-3)=5,解得x=$\frac{5}{m-3}$;
(3) 甲3小时行驶3v km,乙3小时行驶3u km,两地距离为3v+3u=3(v+u) km;
(4) 第1排m个,第2排m+1个,第3排m+2个,...,第n排m+(n-1)=m+n-1个。
2. (1)用含a,b的代数式表示相应图形的面积.
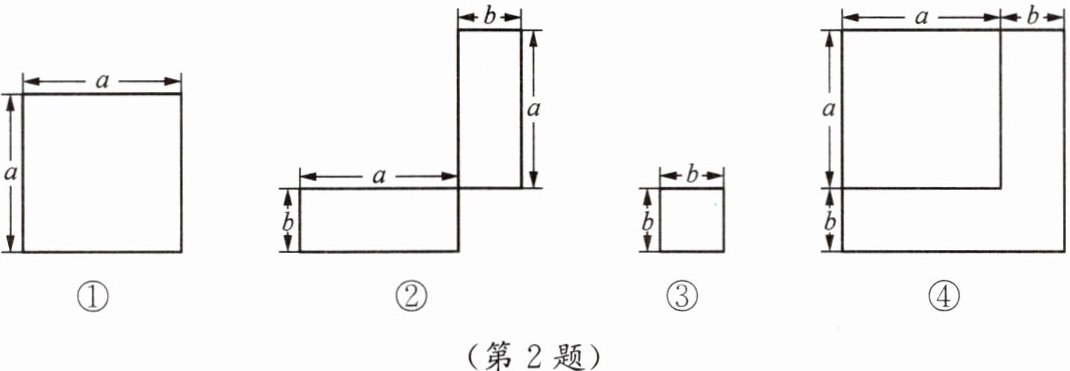
①
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:

①
$a^{2}$
; ②$2ab$
; ③$b^{2}$
; ④$(a+b)^2$.(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:
$a^{2}+2ab+b^{2}=(a+b)^{2}$
.答案:$ $
$ a^{2}$
$2ab$
$ b^{2}$
$a^{2}+2ab+b^{2}=(a+b)^{2}$
$ a^{2}$
$2ab$
$ b^{2}$
$a^{2}+2ab+b^{2}=(a+b)^{2}$