2. 下列几何图形与相应语言描述相符的是(
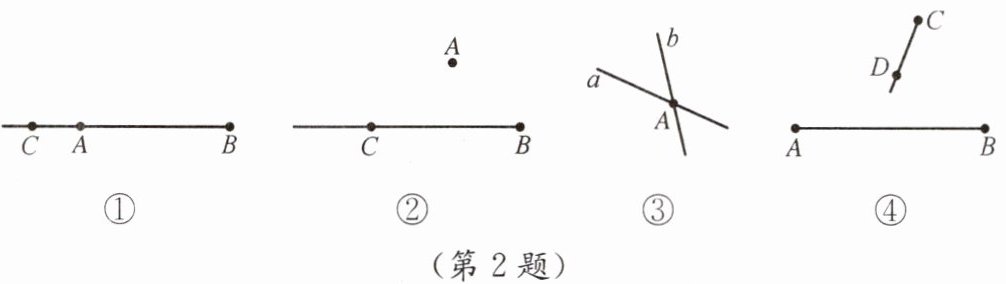
A.如图①所示,延长线段BA到点C
B.如图②所示,射线BC经过点A
C.如图③所示,直线a和直线b相交于点A
D.如图④所示,射线CD和线段AB没有交点
C
)
A.如图①所示,延长线段BA到点C
B.如图②所示,射线BC经过点A
C.如图③所示,直线a和直线b相交于点A
D.如图④所示,射线CD和线段AB没有交点
答案:C
解析:
首先分析选项A:图①中,点C在点A的左边,应该是延长线段AB到点C,而不是延长线段BA到点C,所以A选项错误。
接着分析选项B:图②中,射线BC是从点B出发经过点C的射线,并不经过点A,所以B选项错误。
然后分析选项C:图③中,直线a和直线b相交于点A,描述与图形相符,所以C选项正确。
最后分析选项D:图④中,射线CD是向点D方向无限延伸的,延伸后会与线段AB相交,所以D选项错误。
接着分析选项B:图②中,射线BC是从点B出发经过点C的射线,并不经过点A,所以B选项错误。
然后分析选项C:图③中,直线a和直线b相交于点A,描述与图形相符,所以C选项正确。
最后分析选项D:图④中,射线CD是向点D方向无限延伸的,延伸后会与线段AB相交,所以D选项错误。
3. 如图,图中共有
15
条线段,其中以C为端点的线段是CA,CF,CE,CD,CB
.答案:15
CA,CF,CE,CD,CB
CA,CF,CE,CD,CB
4. 由连云港东到徐州的列车,运行途中停靠的车站依次是连云港东—连云港—东海县—新沂—邳州东—徐州,则这次列车有
15
种不同的票价(往返票价相同),需为这次列车准备30
种车票.答案:15,30
$\frac{n(n-1)}{2}$
$\frac{n(n-1)}{2}$
解析:
连云港东到徐州的列车,运行途中停靠的车站依次是连云港东—连云港—东海县—新沂—邳州东—徐州,共有6个车站。不同的票价对应不同的线段,计算线段数量:$5 + 4 + 3 + 2 + 1 = 15$(种)。车票需考虑方向,数量为线段数量的2倍:$15×2 = 30$(种)。
15;30
15;30
1. 有下列四种生活、生产现象:① 用两根钉子可以把木条固定在墙上;② 植树时,只要先确定两棵树的位置,就能确定同一行树所在的直线;③ 从A地到B地架设电线,总是尽可能沿线段AB架设;④ 把弯曲的公路改直,就能缩短路程.其中,可用“两点之间,线段最短”来解释的现象有(
A.①②
B.①③
C.②④
D.③④
D
)A.①②
B.①③
C.②④
D.③④
答案:D
解析:
①用两根钉子可以把木条固定在墙上,利用的是“两点确定一条直线”;②植树时,只要先确定两棵树的位置,就能确定同一行树所在的直线,利用的是“两点确定一条直线”;③从A地到B地架设电线,总是尽可能沿线段AB架设,利用的是“两点之间,线段最短”;④把弯曲的公路改直,就能缩短路程,利用的是“两点之间,线段最短”。所以可用“两点之间,线段最短”来解释的现象有③④。
2. 如图,直线l上有A,B,C三点,则图中的线段有______条,射线有______条,直线有______条.


答案:
3
6
1
3
6
1

解析:
图中的线段有:AB, BC, AC,共3条。
每一点可以向两个方向发出射线,因此射线有6条。
直线只有1条。
每一点可以向两个方向发出射线,因此射线有6条。
直线只有1条。
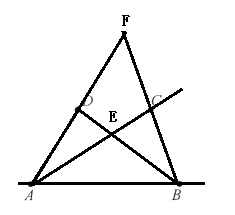
3. 读句画图:
如图,平面内有A,B,C,D四个点.
(1)画直线AB、线段AD、射线AC;
(2)连接BD,BD与射线AC相交于点E;
(3)连接BC,并延长BC,交线段AD的延长线于点F.

如图,平面内有A,B,C,D四个点.
(1)画直线AB、线段AD、射线AC;
(2)连接BD,BD与射线AC相交于点E;
(3)连接BC,并延长BC,交线段AD的延长线于点F.

答案:


4. 同一平面内有四个点,过每两点画一条直线,则可画直线(
A.1条
B.4条
C.6条
D.1条或4条或6条
D
)A.1条
B.4条
C.6条
D.1条或4条或6条
答案:D
解析:
当四个点在同一直线上时,可画直线1条;
当三个点在同一直线上,第四个点不在该直线上时,可画直线4条;
当任意三个点不在同一直线上时,可画直线6条。
故可画直线1条或4条或6条。
D
当三个点在同一直线上,第四个点不在该直线上时,可画直线4条;
当任意三个点不在同一直线上时,可画直线6条。
故可画直线1条或4条或6条。
D
5. 如图,同一平面内2条直线相交,只有1个交点;3条直线两两相交,最多有3个交点;4条直线两两相交,最多有
6
个交点;5条直线两两相交,最多有10
个交点.请你猜想:10条直线两两相交,最多有45
个交点;n条直线两两相交,最多有$\frac{n(n-1)}{2}$
个交点.答案:6
10
45
$\frac{n(n-1)}{2}$
10
45
$\frac{n(n-1)}{2}$
解析:
1. 4条直线两两相交时,每条直线与其他3条直线相交,交点数为3个,4条直线共有4×3个交点,但每个交点被计算了两次,因此交点数为 $\frac{4 × 3}{2} = 6$ 个。
2. 5条直线两两相交时,每条直线与其他4条直线相交,交点数为4个,5条直线共有5×4个交点,但每个交点被计算了两次,因此交点数为 $\frac{5 × 4}{2} = 10$ 个。
3. 猜想10条直线两两相交时,每条直线与其他9条直线相交,交点数为9个,10条直线共有10×9个交点,但每个交点被计算了两次,因此交点数为 $\frac{10 × 9}{2} = 45$ 个。
4. n条直线两两相交时,每条直线与其他n-1条直线相交,交点数为n-1个,n条直线共有n(n-1)个交点,但每个交点被计算了两次,因此交点数为 $\frac{n(n-1)}{2}$ 个。
2. 5条直线两两相交时,每条直线与其他4条直线相交,交点数为4个,5条直线共有5×4个交点,但每个交点被计算了两次,因此交点数为 $\frac{5 × 4}{2} = 10$ 个。
3. 猜想10条直线两两相交时,每条直线与其他9条直线相交,交点数为9个,10条直线共有10×9个交点,但每个交点被计算了两次,因此交点数为 $\frac{10 × 9}{2} = 45$ 个。
4. n条直线两两相交时,每条直线与其他n-1条直线相交,交点数为n-1个,n条直线共有n(n-1)个交点,但每个交点被计算了两次,因此交点数为 $\frac{n(n-1)}{2}$ 个。