3. 某地举办乒乓球比赛的费用 $ y $ 元包括两部分:一部分是租用比赛场地等固定不变的费用 $ b $ 元,另一部分是与参加比赛的人数 $ x $ 人成正比例的费用.已知当 $ x= 20 $ 时, $ y= 1600 $;当 $ x= 30 $ 时, $ y= 2000 $.
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 如果承办此次比赛的组委会共筹集经费 6350 元,那么这次比赛最多可邀请多少名运动员参赛?
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 如果承办此次比赛的组委会共筹集经费 6350 元,那么这次比赛最多可邀请多少名运动员参赛?
答案:(1) 设$y$关于$x$的函数表达式为$y = kx + b$($k \neq 0$)。
根据题意,当$x = 20$时,$y = 1600$;当$x = 30$时,$y = 2000$。
代入得:
$\begin{cases}20k + b = 1600 \\30k + b = 2000\end{cases}$
解这个方程组,两式相减得:
$10k = 400 \implies k = 40$
将$k = 40$代入任一方程得:
$20 × 40 + b = 1600 \implies b = 800$
所以,$y$关于$x$的函数表达式为$y = 40x + 800$。
(2) 已知组委会共筹集经费6350元,即$y = 6350$。
代入$y = 40x + 800$得:
$40x + 800 = 6350$
解这个方程得:
$40x = 5550 \implies x = 138.75$
由于人数必须是整数,所以最多可邀请138名运动员参赛(因为不能邀请非整数名运动员,且经费有限,不能超过6350元)。
根据题意,当$x = 20$时,$y = 1600$;当$x = 30$时,$y = 2000$。
代入得:
$\begin{cases}20k + b = 1600 \\30k + b = 2000\end{cases}$
解这个方程组,两式相减得:
$10k = 400 \implies k = 40$
将$k = 40$代入任一方程得:
$20 × 40 + b = 1600 \implies b = 800$
所以,$y$关于$x$的函数表达式为$y = 40x + 800$。
(2) 已知组委会共筹集经费6350元,即$y = 6350$。
代入$y = 40x + 800$得:
$40x + 800 = 6350$
解这个方程得:
$40x = 5550 \implies x = 138.75$
由于人数必须是整数,所以最多可邀请138名运动员参赛(因为不能邀请非整数名运动员,且经费有限,不能超过6350元)。
1. 已知 $ y $ 与 $ x-2 $ 成正比例,当 $ x= 3 $ 时, $ y= -4 $,则 $ y $ 关于 $ x $ 的函数表达式为
y = -4x + 8
.答案:y = -4x + 8
解析:
1. 根据题意,设 $ y = k(x - 2) $,其中 $ k $ 为比例常数。
2. 当 $ x = 3 $ 时,$ y = -4 $,代入上式得:
$ -4 = k(3 - 2) $
3. 解得 $ k = -4 $。
4. 将 $ k $ 代入原式,得 $ y = -4(x - 2) $。
5. 展开得 $ y = -4x + 8 $。
2. 当 $ x = 3 $ 时,$ y = -4 $,代入上式得:
$ -4 = k(3 - 2) $
3. 解得 $ k = -4 $。
4. 将 $ k $ 代入原式,得 $ y = -4(x - 2) $。
5. 展开得 $ y = -4x + 8 $。
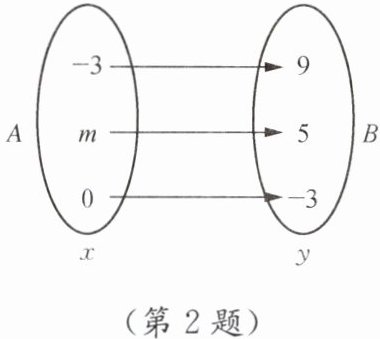
2. 如图,已知 B 中的实数 $ y $ 与 A 中的实数 $ x $ 之间的对应关系是某一个一次函数.
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 求 $ m $ 的值.
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 求 $ m $ 的值.

答案:(1)
设该一次函数表达式为$y = kx + b$。
把$x = -3$,$y = 9$和$x = 0$,$y = -3$代入$y = kx + b$中,
得$\begin{cases}-3k + b = 9 \\b = -3 \end{cases}$
将$b = -3$代入$-3k + b = 9$,得$-3k - 3 = 9$,
$-3k=12$,解得$k = -4$。
所以$y$关于$x$的函数表达式为$y = -4x - 3$。
(2)
当$x = m$时,$y = 5$,把$y = 5$代入$y = -4x - 3$,
得$5 = -4m - 3$,
$4m=-8$,解得$m = -2$。
设该一次函数表达式为$y = kx + b$。
把$x = -3$,$y = 9$和$x = 0$,$y = -3$代入$y = kx + b$中,
得$\begin{cases}-3k + b = 9 \\b = -3 \end{cases}$
将$b = -3$代入$-3k + b = 9$,得$-3k - 3 = 9$,
$-3k=12$,解得$k = -4$。
所以$y$关于$x$的函数表达式为$y = -4x - 3$。
(2)
当$x = m$时,$y = 5$,把$y = 5$代入$y = -4x - 3$,
得$5 = -4m - 3$,
$4m=-8$,解得$m = -2$。
3. 如图,两摞相同规格的碗整齐地叠放在桌面上,请根据图中给出的信息,解答下列问题:
(1) 求整齐叠放在桌面上的碗的高度 $ y $ cm 关于碗数量 $ x $ 个的一次函数表达式;
(2) 若把这两摞碗整齐地叠成一摞,则这摞碗的高度是多少?

(1) 求整齐叠放在桌面上的碗的高度 $ y $ cm 关于碗数量 $ x $ 个的一次函数表达式;
(2) 若把这两摞碗整齐地叠成一摞,则这摞碗的高度是多少?

答案:(1) 设一次函数表达式为 $ y = kx + b $。
由题意,得:
当 $ x = 4 $ 时,$ y = 10.5 $;当 $ x = 5 $ 时,$ y = 12 $。
代入得:
$\begin{cases}4k + b = 10.5 \\5k + b = 12\end{cases}$
解得 $ k = 1.5 $,$ b = 4.5 $。
故函数表达式为 $ y = 1.5x + 4.5 $。
(2) 两摞碗总数为 $ 4 + 5 = 9 $ 个,即 $ x = 9 $。
代入表达式得 $ y = 1.5×9 + 4.5 = 18 $。
(1) $ y = 1.5x + 4.5 $;(2) 18 cm。
由题意,得:
当 $ x = 4 $ 时,$ y = 10.5 $;当 $ x = 5 $ 时,$ y = 12 $。
代入得:
$\begin{cases}4k + b = 10.5 \\5k + b = 12\end{cases}$
解得 $ k = 1.5 $,$ b = 4.5 $。
故函数表达式为 $ y = 1.5x + 4.5 $。
(2) 两摞碗总数为 $ 4 + 5 = 9 $ 个,即 $ x = 9 $。
代入表达式得 $ y = 1.5×9 + 4.5 = 18 $。
(1) $ y = 1.5x + 4.5 $;(2) 18 cm。