活动一:画一画 试一试
阅读课本第 152 页的“讨论”,并思考下列问题:
(1)观察正比例函数 $ y= 2x $,$ y= x $,$ y= -x $,$ y= -\frac{1}{2}x $ 的图象,说说它们从左向右的变化趋势(上升或下降).
(2)点 $ (1,y_1) $,$ (2,y_2) $ 均在函数 $ y= 2x $ 的图象上,试比较 $ y_1,y_2 $ 的大小关系.
(3)点 $ (x_1,y_1) $,$ (x_2,y_2) $ 均在函数 $ y= 2x $ 的图象上,且 $ x_1<x_2 $,试比较 $ y_1,y_2 $ 的大小关系.
(4)点 $ (x_1,y_1) $,$ (x_2,y_2) $ 均在函数 $ y= ax(a>0) $ 的图象上,且 $ x_1<x_2 $,试比较 $ y_1,y_2 $ 的大小关系.
阅读课本第 152 页的“讨论”,并思考下列问题:
(1)观察正比例函数 $ y= 2x $,$ y= x $,$ y= -x $,$ y= -\frac{1}{2}x $ 的图象,说说它们从左向右的变化趋势(上升或下降).
(2)点 $ (1,y_1) $,$ (2,y_2) $ 均在函数 $ y= 2x $ 的图象上,试比较 $ y_1,y_2 $ 的大小关系.
(3)点 $ (x_1,y_1) $,$ (x_2,y_2) $ 均在函数 $ y= 2x $ 的图象上,且 $ x_1<x_2 $,试比较 $ y_1,y_2 $ 的大小关系.
(4)点 $ (x_1,y_1) $,$ (x_2,y_2) $ 均在函数 $ y= ax(a>0) $ 的图象上,且 $ x_1<x_2 $,试比较 $ y_1,y_2 $ 的大小关系.
答案:(1) $y = 2x$,$y = x$ 图象从左向右上升;$y = -x$,$y = -\frac{1}{2}x$ 图象从左向右下降。
(2) $y_1 < y_2$
(3) $y_1 < y_2$
(4) $y_1 < y_2$
(2) $y_1 < y_2$
(3) $y_1 < y_2$
(4) $y_1 < y_2$
解析:
(1) 对于正比例函数 $y = kx$,当 $k > 0$ 时,图象从左向右上升;当 $k < 0$ 时,图象从左向右下降。
$y = 2x$,$k = 2 > 0$,图象从左向右上升;
$y = x$,$k = 1 > 0$,图象从左向右上升;
$y = -x$,$k = -1 < 0$,图象从左向右下降;
$y = -\frac{1}{2}x$,$k = -\frac{1}{2} < 0$,图象从左向右下降。
(2) 因为点 $(1,y_1)$,$(2,y_2)$ 均在函数 $y = 2x$ 的图象上,将 $x = 1$ 代入 $y = 2x$ 得 $y_1 = 2×1 = 2$;将 $x = 2$ 代入 $y = 2x$ 得 $y_2 = 2×2 = 4$,所以 $y_1 < y_2$。
(3) 对于函数 $y = 2x$,$k = 2 > 0$,$y$ 随 $x$ 的增大而增大。已知 $x_1 < x_2$,所以 $y_1 < y_2$。
(4) 对于函数 $y = ax(a > 0)$,$k = a > 0$,$y$ 随 $x$ 的增大而增大。因为 $x_1 < x_2$,所以 $y_1 < y_2$。
$y = 2x$,$k = 2 > 0$,图象从左向右上升;
$y = x$,$k = 1 > 0$,图象从左向右上升;
$y = -x$,$k = -1 < 0$,图象从左向右下降;
$y = -\frac{1}{2}x$,$k = -\frac{1}{2} < 0$,图象从左向右下降。
(2) 因为点 $(1,y_1)$,$(2,y_2)$ 均在函数 $y = 2x$ 的图象上,将 $x = 1$ 代入 $y = 2x$ 得 $y_1 = 2×1 = 2$;将 $x = 2$ 代入 $y = 2x$ 得 $y_2 = 2×2 = 4$,所以 $y_1 < y_2$。
(3) 对于函数 $y = 2x$,$k = 2 > 0$,$y$ 随 $x$ 的增大而增大。已知 $x_1 < x_2$,所以 $y_1 < y_2$。
(4) 对于函数 $y = ax(a > 0)$,$k = a > 0$,$y$ 随 $x$ 的增大而增大。因为 $x_1 < x_2$,所以 $y_1 < y_2$。
活动二:想一想 写一写
正比例函数 $ y= kx $ 的图象经过的象限与 k 的符号的关系:
(1)$ k>0 \iff y= kx $ 的图象经过
(2)$ k<0 \iff y= kx $ 的图象经过
正比例函数 $ y= kx $ 的图象经过的象限与 k 的符号的关系:
(1)$ k>0 \iff y= kx $ 的图象经过
一、三
象限;(2)$ k<0 \iff y= kx $ 的图象经过
二、四
象限.答案:(1) 一、三
(2) 二、四
(2) 二、四
解析:
(1) 当 $k>0$ 时,正比例函数 $y = kx$ 的斜率为正,表示函数图象从左下方向右上方斜着上升,因此图象会经过第一象限和第三象限。
(2) 当 $k<0$ 时,正比例函数 $y = kx$ 的斜率为负,表示函数图象从左上方向右下方斜着下降,因此图象会经过第二象限和第四象限。
(2) 当 $k<0$ 时,正比例函数 $y = kx$ 的斜率为负,表示函数图象从左上方向右下方斜着下降,因此图象会经过第二象限和第四象限。
1. 在平面直角坐标系中,函数 $ y= \frac{4}{5}x $ 的图象大致是(
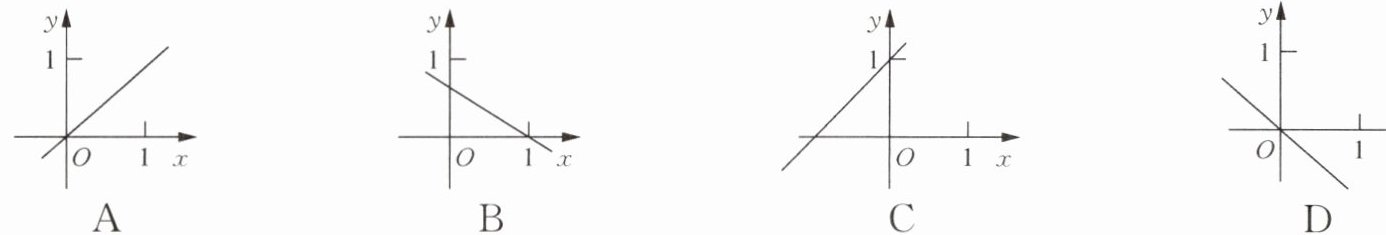
A
) 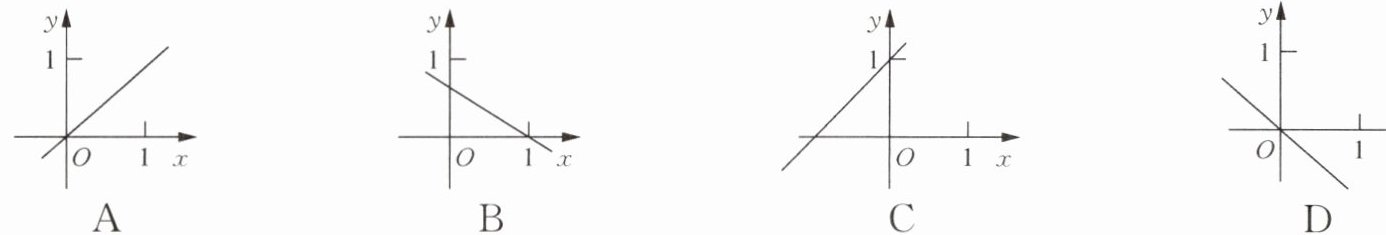
答案:A
解析:
函数 $y=\frac{4}{5} x$ 是一次函数,其图象是一条直线。
一次函数的一般形式为 $y=kx$,其中 $k$ 是斜率。
函数 $y=\frac{4}{5} x$ 的斜率 $k=\frac{4}{5}>0$,因此图象是从左下到右上的直线,且经过原点。
根据斜率为正,可以确定图象经过第一、三象限,且经过原点。
选项A:直线从左下到右上,经过原点,符合 $y=\frac{4}{5} x$ 的图象特征。
选项B:直线从左上到右下,不符合。
选项C:直线从左下到右上,但不经过原点,不符合。
选项D:直线从左上到右下,不符合。
一次函数的一般形式为 $y=kx$,其中 $k$ 是斜率。
函数 $y=\frac{4}{5} x$ 的斜率 $k=\frac{4}{5}>0$,因此图象是从左下到右上的直线,且经过原点。
根据斜率为正,可以确定图象经过第一、三象限,且经过原点。
选项A:直线从左下到右上,经过原点,符合 $y=\frac{4}{5} x$ 的图象特征。
选项B:直线从左上到右下,不符合。
选项C:直线从左下到右上,但不经过原点,不符合。
选项D:直线从左上到右下,不符合。
2. 正比例函数 $ y= kx $(k 是常数,$ k\neq0 $)的图象是一条经过
原点
的直线.答案:原点
解析:
对于正比例函数 $y = kx$(其中 $k$ 是常数,且 $k \neq 0$),当 $x = 0$ 时,$y = 0$。这说明正比例函数的图象必定经过原点。
3. 如图是正比例函数 $ y= kx(k\neq0) $ 的大致图象,写出一个符合题意的 k 的值:

-1
.
答案:-1(答案不唯一,只要是负数即可)
解析:
观察图象可知,该正比例函数图象经过第二、四象限。
对于正比例函数$y = kx(k\neq0)$,当$k\lt0$时,函数图象经过第二、四象限;当$k\gt0$时,函数图象经过第一、三象限。
所以$k\lt0$,那么只要取一个小于$0$的数即可,比如$k = -1$。
对于正比例函数$y = kx(k\neq0)$,当$k\lt0$时,函数图象经过第二、四象限;当$k\gt0$时,函数图象经过第一、三象限。
所以$k\lt0$,那么只要取一个小于$0$的数即可,比如$k = -1$。