4. 在探究某个正比例函数的图象时,小张列出如下表格,则表中 m 的值为______.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -12| -6 | 0 | m | 12 | … |

| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -12| -6 | 0 | m | 12 | … |

6
答案:6
解析:
设正比例函数的解析式为$y = kx$($k\neq0$),
把$x=-1$,$y = - 6$代入$y = kx$,
得$-6=-k$,
解得$k = 6$,
所以正比例函数的解析式为$y = 6x$。
把$x = 1$代入$y = 6x$,
得$y=6×1 = 6$,
即$m = 6$。
把$x=-1$,$y = - 6$代入$y = kx$,
得$-6=-k$,
解得$k = 6$,
所以正比例函数的解析式为$y = 6x$。
把$x = 1$代入$y = 6x$,
得$y=6×1 = 6$,
即$m = 6$。
5. 甲、乙两人赛跑,路程 s m 与时间 t s 之间的关系如图所示,则下列说法正确的是
① 两人赛跑的路程是 100 m;
② 甲先到达终点;
③ 甲跑的平均速度比乙跑的平均速度快 0.5 m/s;
④ 乙跑的平均速度是 8 m/s.

①②④
.(填序号)① 两人赛跑的路程是 100 m;
② 甲先到达终点;
③ 甲跑的平均速度比乙跑的平均速度快 0.5 m/s;
④ 乙跑的平均速度是 8 m/s.

答案:①②④
解析:
① 由图可知,纵坐标表示路程,两人赛跑的路程达到100m,故①正确;
② 由图可知,甲到达终点所用的时间是12s,乙到达终点所用的时间是12.5s,所以甲先到达终点,故②正确;
③ 甲的平均速度:$v_{甲} = \frac{100}{12} = \frac{25}{3}$ (m/s),乙的平均速度:$v_{乙} = \frac{100}{12.5} = 8$ (m/s),$v_{甲} - v_{乙} = \frac{25}{3} - 8 = \frac{1}{3}$ (m/s),故③错误;
④ 乙跑的平均速度是8m/s,故④正确。
② 由图可知,甲到达终点所用的时间是12s,乙到达终点所用的时间是12.5s,所以甲先到达终点,故②正确;
③ 甲的平均速度:$v_{甲} = \frac{100}{12} = \frac{25}{3}$ (m/s),乙的平均速度:$v_{乙} = \frac{100}{12.5} = 8$ (m/s),$v_{甲} - v_{乙} = \frac{25}{3} - 8 = \frac{1}{3}$ (m/s),故③错误;
④ 乙跑的平均速度是8m/s,故④正确。
1. 如图,三个正比例函数的图象分别对应的表达式是 $ y= ax $,$ y= bx $,$ y= cx $,将 a,b,c 按从大到小的顺序排列,并用“>”连接:

$b\gt a\gt c$
.
答案:$b\gt a\gt c$
解析:
正比例函数的一般形式为$y = kx$($k$是常数,$k\neq0$),当$k\gt0$时,函数图象经过一、三象限,且$k$越大,图象越靠近$y$轴;当$k\lt0$时,函数图象经过二、四象限。
观察图象可知,$y = bx$和$y = ax$的图象经过一、三象限,所以$a\gt0$,$b\gt0$,且$y = bx$的图象比$y = ax$的图象更靠近$y$轴,所以$b\gt a\gt0$。
$y = cx$的图象经过二、四象限,所以$c\lt0$。
因此,$b\gt a\gt c$。
观察图象可知,$y = bx$和$y = ax$的图象经过一、三象限,所以$a\gt0$,$b\gt0$,且$y = bx$的图象比$y = ax$的图象更靠近$y$轴,所以$b\gt a\gt0$。
$y = cx$的图象经过二、四象限,所以$c\lt0$。
因此,$b\gt a\gt c$。
2. 某型号汽油的油量与相应金额的关系如图所示,小明爸爸一次加这种型号的汽油 40 L,需要付加油站

299.6
元.
答案:299.6
解析:
设汽油的油量为$x L$,相应金额为$y$元,$y$与$x$是一次函数关系,设$y = kx$(因为图象过原点)。
把$x = 100$,$y = 749$代入$y = kx$,得$749 = 100k$,解得$k = 7.49$,所以$y = 7.49x$。
当$x = 40$时,$y = 7.49×40 = 299.6$(元)。
把$x = 100$,$y = 749$代入$y = kx$,得$749 = 100k$,解得$k = 7.49$,所以$y = 7.49x$。
当$x = 40$时,$y = 7.49×40 = 299.6$(元)。
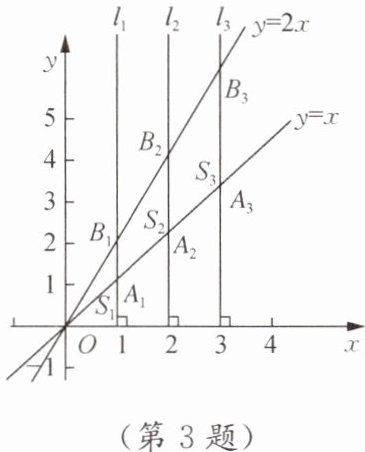
3. 如图,直线 $ l_1\perp x $ 轴,垂足为 $ (1,0) $;直线 $ l_2\perp x $ 轴,垂足为 $ (2,0) $;直线 $ l_3\perp x $ 轴,垂足为 $ (3,0) $……直线 $ l_n\perp x $ 轴,垂足为 $ (n,0) $(其中 n 为正整数). 函数 $ y= x $ 的图象与直线 $ l_1,l_2,l_3,…,l_n $ 分别交于点 $ A_1,A_2,A_3,…,A_n $;函数 $ y= 2x $ 的图象与直线 $ l_1,l_2,l_3,…,l_n $ 分别交于点 $ B_1,B_2,B_3,…,B_n $. 如果 $ \triangle OA_1B_1 $ 的面积记作 $ S_1 $,四边形 $ A_1A_2B_2B_1 $ 的面积记作 $ S_2 $,四边形 $ A_2A_3B_3B_2 $ 的面积记作 $ S_3 $……四边形 $ A_{n-1}A_nB_nB_{n-1} $ 的面积记作 $ S_n $,那么 $ S_{2024}= $
$\frac{4047}{2}$
.
答案:$\frac{4047}{2}$
解析:
由题意,直线$ l_k \perp x $轴且垂足为$(k,0)$,故$ l_k $的方程为$ x=k $。
函数$ y=x $与$ l_k $交于点$ A_k $,则$ A_k(k,k) $;函数$ y=2x $与$ l_k $交于点$ B_k $,则$ B_k(k,2k) $。
对于四边形$ A_{k-1}A_kB_kB_{k-1} $($ k \geq 2 $):
上底$ A_{k-1}B_{k-1} $的长度为$ 2(k-1)-(k-1)=k-1 $;
下底$ A_kB_k $的长度为$ 2k - k = k $;
两底间距离(高)为$ k - (k-1) = 1 $。
其面积$ S_k = \frac{(上底 + 下底) × 高}{2} = \frac{(k-1 + k) × 1}{2} = \frac{2k - 1}{2} $。
当$ k = 2024 $时,$ S_{2024} = \frac{2 × 2024 - 1}{2} = \frac{4047}{2} $。