14. (10分)根据材料解答:
$\because \sqrt{4}<\sqrt{5}<\sqrt{9}$,即$2<\sqrt{5}<3$,$\therefore \sqrt{5}$的整数部分为2,小数部分为$\sqrt{5}-2$。
(1)$\sqrt{11}$的整数部分是
(2)若$\sqrt{17}$的小数部分为m,$\sqrt{11}-1$的整数部分为n,求$m+n-\sqrt{17}$的值。
$\because \sqrt{4}<\sqrt{5}<\sqrt{9}$,即$2<\sqrt{5}<3$,$\therefore \sqrt{5}$的整数部分为2,小数部分为$\sqrt{5}-2$。
(1)$\sqrt{11}$的整数部分是
3
;(2)若$\sqrt{17}$的小数部分为m,$\sqrt{11}-1$的整数部分为n,求$m+n-\sqrt{17}$的值。
答案:(1)
∵$\sqrt{9} \lt \sqrt{11} \lt \sqrt{16}$,即$3 \lt \sqrt{11} \lt 4$,
∴$\sqrt{11}$的整数部分是3。
(2)
∵$\sqrt{16} \lt \sqrt{17} \lt \sqrt{25}$,即$4 \lt \sqrt{17} \lt 5$,
∴$\sqrt{17}$的整数部分是4,小数部分$m = \sqrt{17} - 4$。
∵$\sqrt{9} \lt \sqrt{11} \lt \sqrt{16}$,即$3 \lt \sqrt{11} \lt 4$,
∴$2 \lt \sqrt{11} - 1 \lt 3$,
∴$\sqrt{11} - 1$的整数部分$n = 2$。
∴$m + n - \sqrt{17} = \sqrt{17} - 4 + 2 - \sqrt{17} = -2$。
∵$\sqrt{9} \lt \sqrt{11} \lt \sqrt{16}$,即$3 \lt \sqrt{11} \lt 4$,
∴$\sqrt{11}$的整数部分是3。
(2)
∵$\sqrt{16} \lt \sqrt{17} \lt \sqrt{25}$,即$4 \lt \sqrt{17} \lt 5$,
∴$\sqrt{17}$的整数部分是4,小数部分$m = \sqrt{17} - 4$。
∵$\sqrt{9} \lt \sqrt{11} \lt \sqrt{16}$,即$3 \lt \sqrt{11} \lt 4$,
∴$2 \lt \sqrt{11} - 1 \lt 3$,
∴$\sqrt{11} - 1$的整数部分$n = 2$。
∴$m + n - \sqrt{17} = \sqrt{17} - 4 + 2 - \sqrt{17} = -2$。
15. (10分)根据爱因斯坦相对论时间的相对性原理,物体在高速运动的情况下时间会延缓(时钟变慢),当地面上的人经过1s时,宇宙飞船高速飞行的人只经过$\sqrt{1-\left(\frac{v}{c}\right)^{2}}$s(c是光速,为$3× 10^{8}\ m/s$,v是宇宙飞船的速度)。假定有一对兄弟,哥哥18岁,弟弟15岁,哥哥乘着宇宙飞船做星际旅行,设该宇宙飞船的速度是光速的0.98倍。问:弟弟20岁时,刚从宇宙旅行回来的哥哥是几岁?
答案:1. 弟弟经历的时间:$\Delta t = 20 - 15 = 5$年。
2. 飞船速度$v = 0.98c$,则$\frac{v}{c} = 0.98$,$(\frac{v}{c})^2 = 0.98^2 = 0.9604$。
3. 计算$1 - (\frac{v}{c})^2 = 1 - 0.9604 = 0.0396$。
4. 时间延缓因子:$\sqrt{1 - (\frac{v}{c})^2} = \sqrt{0.0396} \approx 0.199$。
5. 哥哥在飞船上经历的时间:$\Delta t' = \Delta t × \sqrt{1 - (\frac{v}{c})^2} \approx 5 × 0.199 = 0.995$年≈1年。
6. 哥哥回来时的年龄:$18 + 0.995 \approx 19$岁。
结论:19岁。
2. 飞船速度$v = 0.98c$,则$\frac{v}{c} = 0.98$,$(\frac{v}{c})^2 = 0.98^2 = 0.9604$。
3. 计算$1 - (\frac{v}{c})^2 = 1 - 0.9604 = 0.0396$。
4. 时间延缓因子:$\sqrt{1 - (\frac{v}{c})^2} = \sqrt{0.0396} \approx 0.199$。
5. 哥哥在飞船上经历的时间:$\Delta t' = \Delta t × \sqrt{1 - (\frac{v}{c})^2} \approx 5 × 0.199 = 0.995$年≈1年。
6. 哥哥回来时的年龄:$18 + 0.995 \approx 19$岁。
结论:19岁。
16. (10分)如图,用两张面积为$8\ cm^{2}$的小正方形纸片剪拼成一个大正方形纸片。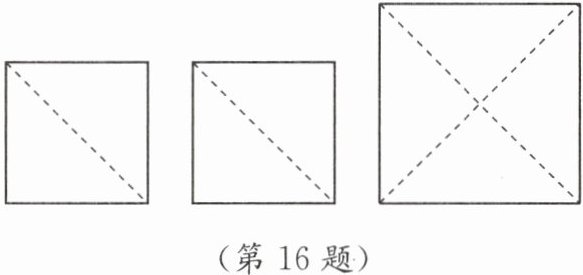
(1)大正方形纸片的边长是
(2)若沿此大正方形纸片边的方向剪一个长方形,能否剪出长与宽之比为3:2,面积为$12\ cm^{2}$的长方形纸片?若能,求出该长方形纸片的长和宽;若不能,说明理由。(参考数据:$\sqrt{2}\approx 1.414$,$\sqrt{3}\approx 1.732$)

(1)大正方形纸片的边长是
4
cm;(2)若沿此大正方形纸片边的方向剪一个长方形,能否剪出长与宽之比为3:2,面积为$12\ cm^{2}$的长方形纸片?若能,求出该长方形纸片的长和宽;若不能,说明理由。(参考数据:$\sqrt{2}\approx 1.414$,$\sqrt{3}\approx 1.732$)
解:设长方形纸片的长为$3x\ cm$,宽为$2x\ cm$。根据题意,长方形的面积为$3x\cdot 2x=12\ cm^2$,解得$x=\sqrt{2}\ cm$。长方形的长为$3\sqrt{2}\ cm$,宽为$2\sqrt{2}\ cm$。因为$3\sqrt{2}\approx 4.242\gt 4$,所以不能剪出符合要求的长方形。
答案:解:
(1) 大正方形的面积为 $8×2=16\ cm^2$,所以边长为 $\sqrt{16}=4\ cm$。
故答案为:4;
(2) 设长方形纸片的长为 $3x\ cm$,宽为 $2x\ cm$。
根据题意,长方形的面积为 $3x\cdot 2x=12\ cm^2$,解得 $x=\sqrt{2}\ cm$。
长方形的长为 $3\sqrt{2}\ cm$,宽为 $2\sqrt{2}\ cm$。
因为 $3\sqrt{2}\approx 4.242\gt 4$,所以不能剪出符合要求的长方形。
(1) 大正方形的面积为 $8×2=16\ cm^2$,所以边长为 $\sqrt{16}=4\ cm$。
故答案为:4;
(2) 设长方形纸片的长为 $3x\ cm$,宽为 $2x\ cm$。
根据题意,长方形的面积为 $3x\cdot 2x=12\ cm^2$,解得 $x=\sqrt{2}\ cm$。
长方形的长为 $3\sqrt{2}\ cm$,宽为 $2\sqrt{2}\ cm$。
因为 $3\sqrt{2}\approx 4.242\gt 4$,所以不能剪出符合要求的长方形。