1. 下列几组数中,不能作为直角三角形三边长的是 (
A.6,8,10
B.5,12,14
C.3,4,5
D.1,2,$\sqrt{3}$
B
)A.6,8,10
B.5,12,14
C.3,4,5
D.1,2,$\sqrt{3}$
答案:B
解析:
对于选项A,有$6^2 + 8^2 = 36 + 64 = 100 = 10^2$,满足勾股定理,故能作为直角三角形三边长。
对于选项B,有$5^2 + 12^2 = 25 + 144 = 169 \neq 14^2$,不满足勾股定理,故不能作为直角三角形三边长。
对于选项C,有$3^2 + 4^2 = 9 + 16 = 25 = 5^2$,满足勾股定理,故能作为直角三角形三边长。
对于选项D,有$1^2 + (\sqrt{3})^2 = 1 + 3 = 4 = 2^2$,满足勾股定理,故能作为直角三角形三边长。
对于选项B,有$5^2 + 12^2 = 25 + 144 = 169 \neq 14^2$,不满足勾股定理,故不能作为直角三角形三边长。
对于选项C,有$3^2 + 4^2 = 9 + 16 = 25 = 5^2$,满足勾股定理,故能作为直角三角形三边长。
对于选项D,有$1^2 + (\sqrt{3})^2 = 1 + 3 = 4 = 2^2$,满足勾股定理,故能作为直角三角形三边长。
2. 小强量得家中计算机显示器的长为61 cm,宽为35 cm,这台显示器尺寸(对角线长)大约为 (
A.16英寸(43 cm)
B.21英寸(54 cm)
C.27英寸(70 cm)
D.32英寸(83 cm)
C
)A.16英寸(43 cm)
B.21英寸(54 cm)
C.27英寸(70 cm)
D.32英寸(83 cm)
答案:C
解析:
根据勾股定理,显示器的对角线长度可以通过其长和宽计算得出。设长为 $a = 61 cm$,宽为 $b = 35 cm$,对角线为 $c$,则:
$c = \sqrt{a^2 + b^2} = \sqrt{61^2 + 35^2} = \sqrt{3721 + 1225} = \sqrt{4946} \approx 70.33 cm$
将计算出的对角线长度与选项中的尺寸进行比较,70.33 cm 最接近 70 cm,即 27 英寸。
$c = \sqrt{a^2 + b^2} = \sqrt{61^2 + 35^2} = \sqrt{3721 + 1225} = \sqrt{4946} \approx 70.33 cm$
将计算出的对角线长度与选项中的尺寸进行比较,70.33 cm 最接近 70 cm,即 27 英寸。
3. 已知等腰三角形的腰长为5,底边长为6,则其面积为 (
A.48
B.24
C.12
D.16
C
)A.48
B.24
C.12
D.16
答案:C
解析:
1. 设等腰三角形为 $ \triangle ABC $,其中 $ AB = AC = 5 $,底边 $ BC = 6 $。
2. 作 $ AD $ 垂直于 $ BC $ 于点 $ D $,则 $ D $ 为 $ BC $ 的中点,因此 $ BD = DC = \frac{BC}{2} = 3 $。
3. 在直角三角形 $ \triangle ABD $ 中,利用勾股定理计算 $ AD $ 的长度:
$ AD = \sqrt{AB^2 - BD^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $。
4. 计算三角形的面积:
$ S_{\triangle ABC} = \frac{1}{2} × BC × AD = \frac{1}{2} × 6 × 4 = 12 $。
2. 作 $ AD $ 垂直于 $ BC $ 于点 $ D $,则 $ D $ 为 $ BC $ 的中点,因此 $ BD = DC = \frac{BC}{2} = 3 $。
3. 在直角三角形 $ \triangle ABD $ 中,利用勾股定理计算 $ AD $ 的长度:
$ AD = \sqrt{AB^2 - BD^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $。
4. 计算三角形的面积:
$ S_{\triangle ABC} = \frac{1}{2} × BC × AD = \frac{1}{2} × 6 × 4 = 12 $。
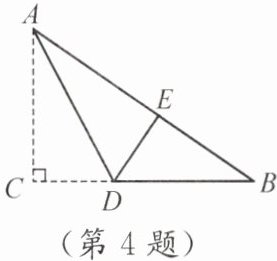
4. 如图,在直角三角形纸片中,$\angle C= 90^{\circ}$,$AC= 6\,cm$,$BC= 8\,cm$,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则BD等于 (
A.2 cm
B.3 cm
C.4 cm
D.5 cm
D
)
A.2 cm
B.3 cm
C.4 cm
D.5 cm
答案:D
解析:
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 6cm$,$BC = 8cm$,根据勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10cm$。
由折叠可知$AE = AC = 6cm$,$DE = CD$,$\angle AED=\angle C = 90^{\circ}$,则$BE=AB - AE=10 - 6 = 4cm$。
设$BD = x cm$,则$CD = DE=(8 - x)cm$。
在$Rt\triangle BDE$中,根据勾股定理$DE^{2}+BE^{2}=BD^{2}$,即$(8 - x)^{2}+4^{2}=x^{2}$。
展开得$64-16x+x^{2}+16 = x^{2}$,移项化简得$16x = 80$,解得$x = 5$,所以$BD = 5cm$。
由折叠可知$AE = AC = 6cm$,$DE = CD$,$\angle AED=\angle C = 90^{\circ}$,则$BE=AB - AE=10 - 6 = 4cm$。
设$BD = x cm$,则$CD = DE=(8 - x)cm$。
在$Rt\triangle BDE$中,根据勾股定理$DE^{2}+BE^{2}=BD^{2}$,即$(8 - x)^{2}+4^{2}=x^{2}$。
展开得$64-16x+x^{2}+16 = x^{2}$,移项化简得$16x = 80$,解得$x = 5$,所以$BD = 5cm$。
5. 数
15
能与12,9组成一组勾股数.答案:所求的勾股数为$15$。
解析:
设所求的数为$x$,
根据勾股定理,若$x$是斜边,则有:
$x^2 = 12^2 + 9^2$,
$x^2 = 144 + 81$,
$x^2 = 225$,
从中解得:$x = 15$ (负值舍去,因为长度不能为负),
若$x$不是斜边,$12$是斜边,则有:
$12^2=x^2+9^2$,
$x^2=144-81$,
$x^2 = 63$,
$x=\sqrt{63}=3\sqrt{7}$,$3\sqrt{7}$不是整数,
由于题目要求的是勾股数,即必须是正整数,且根据勾股数的定义,斜边应该是最大的那个数,
所以,只有$x = 15$满足条件。
根据勾股定理,若$x$是斜边,则有:
$x^2 = 12^2 + 9^2$,
$x^2 = 144 + 81$,
$x^2 = 225$,
从中解得:$x = 15$ (负值舍去,因为长度不能为负),
若$x$不是斜边,$12$是斜边,则有:
$12^2=x^2+9^2$,
$x^2=144-81$,
$x^2 = 63$,
$x=\sqrt{63}=3\sqrt{7}$,$3\sqrt{7}$不是整数,
由于题目要求的是勾股数,即必须是正整数,且根据勾股数的定义,斜边应该是最大的那个数,
所以,只有$x = 15$满足条件。
6. 如图,正方形A,B的面积分别为10,12,则正方形F的面积为______.


22
答案:22
解析:
根据勾股定理和正方形的性质,我们知道:
正方形A的面积为$a^2=10$,
正方形B的面积为$b^2=12$,
正方形F的面积为$c^2$,
由图可知$a^2+b^2=c^2$,
所以$c^2=10+12=22$。
正方形A的面积为$a^2=10$,
正方形B的面积为$b^2=12$,
正方形F的面积为$c^2$,
由图可知$a^2+b^2=c^2$,
所以$c^2=10+12=22$。
7. 在$Rt\triangle ABC$中,$BC= 3$,$AC= 4$,则$AB= $
$5$或$\sqrt{7}$
.答案:$5$或$\sqrt{7}$
解析:
在$Rt\triangle ABC$中,已知$BC = 3$,$AC = 4$,分两种情况讨论:
1. 当$BC$和$AC$为直角边时,根据勾股定理$AB^{2}=BC^{2}+AC^{2}$,将$BC = 3$,$AC = 4$代入可得$AB=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
2. 当$AC$为斜边,$BC$为直角边时,根据勾股定理$AB^{2}=AC^{2}-BC^{2}$,将$BC = 3$,$AC = 4$代入可得$AB=\sqrt{4^{2}-3^{2}}=\sqrt{16 - 9}=\sqrt{7}$。
1. 当$BC$和$AC$为直角边时,根据勾股定理$AB^{2}=BC^{2}+AC^{2}$,将$BC = 3$,$AC = 4$代入可得$AB=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
2. 当$AC$为斜边,$BC$为直角边时,根据勾股定理$AB^{2}=AC^{2}-BC^{2}$,将$BC = 3$,$AC = 4$代入可得$AB=\sqrt{4^{2}-3^{2}}=\sqrt{16 - 9}=\sqrt{7}$。
8. 如图,若小方格的边长为1,则$\triangle ABC$的面积是

7
.
答案:7
解析:
第一步,确定$\triangle ABC$的顶点坐标:
从图中可以看出,小方格的边长为1,所以可以确定:
$A(2,0)$,$B(6,4)$,$C(0,3)$。
第二步,使用面积公式:
可以利用顶点坐标来计算三角形的面积,公式为:
$面积=\frac{1}{2}\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|$。
将$A(2,0)$,$B(6,4)$,$C(0,3)$代入公式:
$面积=\frac{1}{2}\left|2(4-3)+6(3-0)+0(0-4)\right|$
$=\frac{1}{2}\left|2×1+6×3+0×(-4)\right|$
$=\frac{1}{2}\left|2+18\right|$
$=\frac{1}{2}×20$
$=10-3=7$
$面积=\frac{1}{2}\left|8+0+6-0-12+0\right|=\frac{1}{2}\left|14-3× 4\right|= \frac{1}{2}× \left|20-6\right|× \frac{1}{2}= \frac{1}{2}\left|20-6\right|× \frac{1}{2}=3.5× 2= 13-6=7$
不过通过直接数格子也可以得到。
通过数方格的方法,可以数出$\triangle ABC$大约占据了3.5个完整方格的2倍面积(因为底边和高度跨越了多个方格),再减去周围小三角形的面积,最终得到$\triangle ABC$的面积为3.5$×$ 2=7。
从图中可以看出,小方格的边长为1,所以可以确定:
$A(2,0)$,$B(6,4)$,$C(0,3)$。
第二步,使用面积公式:
可以利用顶点坐标来计算三角形的面积,公式为:
$面积=\frac{1}{2}\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|$。
将$A(2,0)$,$B(6,4)$,$C(0,3)$代入公式:
$面积=\frac{1}{2}\left|2(4-3)+6(3-0)+0(0-4)\right|$
$=\frac{1}{2}\left|2×1+6×3+0×(-4)\right|$
$=\frac{1}{2}\left|2+18\right|$
$=\frac{1}{2}×20$
$=10-3=7$
$面积=\frac{1}{2}\left|8+0+6-0-12+0\right|=\frac{1}{2}\left|14-3× 4\right|= \frac{1}{2}× \left|20-6\right|× \frac{1}{2}= \frac{1}{2}\left|20-6\right|× \frac{1}{2}=3.5× 2= 13-6=7$
不过通过直接数格子也可以得到。
通过数方格的方法,可以数出$\triangle ABC$大约占据了3.5个完整方格的2倍面积(因为底边和高度跨越了多个方格),再减去周围小三角形的面积,最终得到$\triangle ABC$的面积为3.5$×$ 2=7。
9. 如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$AC= 9$,$BC= 12$,则点C到AB的距离是

7.2
.
答案:7.2
解析:
在直角三角形$ABC$中,$\angle C=90^\circ$,$AC=9$,$BC=12$。
根据勾股定理,$AB=\sqrt{AC^2+BC^2}=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15$。
设点$C$到$AB$的距离为$h$。
根据三角形面积公式,$S=\frac{1}{2}× AC× BC=\frac{1}{2}× AB× h$。
即$\frac{1}{2}× 9× 12=\frac{1}{2}× 15× h$。
化简得$108=15h$。
解得$h=\frac{108}{15}=7.2$。
所以,点$C$到$AB$的距离是$7.2$。
根据勾股定理,$AB=\sqrt{AC^2+BC^2}=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15$。
设点$C$到$AB$的距离为$h$。
根据三角形面积公式,$S=\frac{1}{2}× AC× BC=\frac{1}{2}× AB× h$。
即$\frac{1}{2}× 9× 12=\frac{1}{2}× 15× h$。
化简得$108=15h$。
解得$h=\frac{108}{15}=7.2$。
所以,点$C$到$AB$的距离是$7.2$。
10. 已知甲、乙两个人从同一地点出发,甲往东走了4 km,乙往南走了3 km,这时甲、乙两人相距
5
km.答案:5
解析:
甲往东走,乙往南走,两人行走的方向构成直角,因此甲、乙两人与出发点构成直角三角形。其中甲走的距离为一条直角边,长度为4km,乙走的距离为另一条直角边,长度为3km。根据勾股定理,斜边(即甲、乙两人之间的距离)的平方等于两直角边的平方和。设甲、乙两人之间的距离为$c$,则有$c^2 = 4^2 + 3^2 = 16 + 9 = 25$,解得$c = \sqrt{25} = 5$。
11. (10分)如图,在长方形纸片ABCD中,$AD= 4\,cm$,$AB= 10\,cm$,按如图的方式折叠,使点B与点D重合,折痕为EF,求DE的长.


答案:设DE的长为$x\,cm$。
由折叠性质知,$BE = DE = x\,cm$。
因为四边形$ABCD$是长方形,所以$AB = 10\,cm$,$\angle A = 90^\circ$,则$AE = AB - BE = (10 - x)\,cm$。
在$Rt\triangle ADE$中,$AD = 4\,cm$,由勾股定理得:
$AD^2 + AE^2 = DE^2$
即$4^2 + (10 - x)^2 = x^2$
展开得$16 + 100 - 20x + x^2 = x^2$
化简得$116 - 20x = 0$
解得$x = \frac{29}{5}$
答:$DE$的长为$\frac{29}{5}\,cm$。
由折叠性质知,$BE = DE = x\,cm$。
因为四边形$ABCD$是长方形,所以$AB = 10\,cm$,$\angle A = 90^\circ$,则$AE = AB - BE = (10 - x)\,cm$。
在$Rt\triangle ADE$中,$AD = 4\,cm$,由勾股定理得:
$AD^2 + AE^2 = DE^2$
即$4^2 + (10 - x)^2 = x^2$
展开得$16 + 100 - 20x + x^2 = x^2$
化简得$116 - 20x = 0$
解得$x = \frac{29}{5}$
答:$DE$的长为$\frac{29}{5}\,cm$。