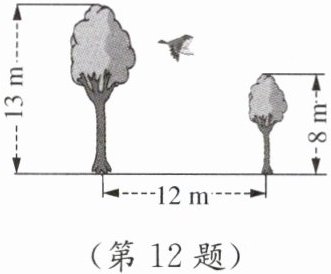
12. (13分)如图,一只小鸟从小树树顶飞到大树树顶上,它飞行的最短路程是多少?(先画出示意图,然后再求解)

答案:因为两点之间,线段最短,所以,小鸟从小树树顶飞到大树树顶的最短路程为线段。
由题可知,小树高度为$8$米,大树高度为$13$米,两树水平距离为$12$米,
所以,水平距离、高度差、飞行路径构成直角三角形,高度差为:$13 - 8 = 5$(米)
设飞行路径为$x$米,
根据勾股定理可得:
$x^2=12^2 + 5^2 $,
$x^2=144 + 25 $,
$x^2=169$,
$x = 13$。
所以它飞行的最短路程是$13$米。
由题可知,小树高度为$8$米,大树高度为$13$米,两树水平距离为$12$米,
所以,水平距离、高度差、飞行路径构成直角三角形,高度差为:$13 - 8 = 5$(米)
设飞行路径为$x$米,
根据勾股定理可得:
$x^2=12^2 + 5^2 $,
$x^2=144 + 25 $,
$x^2=169$,
$x = 13$。
所以它飞行的最短路程是$13$米。
13. (13分)剪若干个大小、形状完全相同的直角三角形,三边长分别记为a,b,c(图①);分别用4张这样的直角三角形纸片拼成图②、图③所示的形状.图②中两个小正方形的面积$S_2$,$S_3$与图③中小正方形的面积$S_1$有什么关系?你能得到a,b,c之间有什么关系?


答案:S₂ + S₃ = S₁;a² + b² = c²。
解析:
图②中,两个小正方形面积分别为S₂ = a²,S₃ = b²,4个直角三角形面积和为4×(1/2)ab = 2ab,故图②总面积为S₂ + S₃ + 2ab = a² + b² + 2ab。
图③中,小正方形S₁的边长为c(直角三角形斜边),面积S₁ = c²,4个直角三角形面积和为2ab,故图③总面积为S₁ + 2ab = c² + 2ab。
因图②与图③均由4个全等直角三角形拼成,总面积相等,即a² + b² + 2ab = c² + 2ab,化简得S₂ + S₃ = S₁,且a² + b² = c²。
解析:
图②中,两个小正方形面积分别为S₂ = a²,S₃ = b²,4个直角三角形面积和为4×(1/2)ab = 2ab,故图②总面积为S₂ + S₃ + 2ab = a² + b² + 2ab。
图③中,小正方形S₁的边长为c(直角三角形斜边),面积S₁ = c²,4个直角三角形面积和为2ab,故图③总面积为S₁ + 2ab = c² + 2ab。
因图②与图③均由4个全等直角三角形拼成,总面积相等,即a² + b² + 2ab = c² + 2ab,化简得S₂ + S₃ = S₁,且a² + b² = c²。
14. (14分)我们知道,凡是可以构成一个直角三角形三边的一组正整数,都是勾股数.比如3,4,5或11,60,61等.
(1) 请你写出一组勾股数:7,
(2) 清朝数学家罗士琳提出了四个构造勾股数的法则,其中有两个法则如下:
(Ⅰ)如果k是大于1的奇数,那么$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$是一组勾股数.
(Ⅱ)如果k是大于2的偶数,那么$k$,$(\frac{k}{2})^2-1$,$(\frac{k}{2})^2+1$是一组勾股数.
① 已知在一组勾股数中,其中有一个数为12,根据以上两个法则分别求出另外两个数;
② 请你从这两个法则中选择一个,并证明它是正确的.
(1) 请你写出一组勾股数:7,
24
,25
.(2) 清朝数学家罗士琳提出了四个构造勾股数的法则,其中有两个法则如下:
(Ⅰ)如果k是大于1的奇数,那么$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$是一组勾股数.
(Ⅱ)如果k是大于2的偶数,那么$k$,$(\frac{k}{2})^2-1$,$(\frac{k}{2})^2+1$是一组勾股数.
① 已知在一组勾股数中,其中有一个数为12,根据以上两个法则分别求出另外两个数;
② 请你从这两个法则中选择一个,并证明它是正确的.
①
Ⅰ. 当$k=12$时,不满足法则(Ⅰ)($k$需为奇数),舍去;
法则(Ⅱ):
$k=12$,则
$\left(\frac{12}{2}\right)^2 - 1 = 35$,
$\left(\frac{12}{2}\right)^2 + 1 = 37$,
故另外两个数为35,37。
Ⅱ. 当$\frac{k^2-1}{2}=12$时,解得$k=5$($k$为奇数),
则$\frac{k^2+1}{2} = 13$,
故另外两个数为5,13。
综上,另外两个数为35,37或5,13。
②
证明法则(Ⅰ):
设$k$为大于1的奇数,则
$k^2 + \left(\frac{k^2-1}{2}\right)^2 = k^2 + \frac{k^4 - 2k^2 + 1}{4} = \frac{k^4 + 2k^2 + 1}{4} = \left(\frac{k^2+1}{2}\right)^2$,
故$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$构成勾股数。
或证明法则(Ⅱ):
设$k$为大于2的偶数,则
$k^2 + \left(\left(\frac{k}{2}\right)^2 - 1\right)^2 = k^2 + \left(\frac{k^2}{4} - 1\right)^2 = \frac{k^4}{16} + \frac{k^2}{2} + 1 = \left(\left(\frac{k}{2}\right)^2 + 1\right)^2$,
故$k$,$\left(\frac{k}{2}\right)^2 - 1$,$\left(\frac{k}{2}\right)^2 + 1$构成勾股数。
Ⅰ. 当$k=12$时,不满足法则(Ⅰ)($k$需为奇数),舍去;
法则(Ⅱ):
$k=12$,则
$\left(\frac{12}{2}\right)^2 - 1 = 35$,
$\left(\frac{12}{2}\right)^2 + 1 = 37$,
故另外两个数为35,37。
Ⅱ. 当$\frac{k^2-1}{2}=12$时,解得$k=5$($k$为奇数),
则$\frac{k^2+1}{2} = 13$,
故另外两个数为5,13。
综上,另外两个数为35,37或5,13。
②
证明法则(Ⅰ):
设$k$为大于1的奇数,则
$k^2 + \left(\frac{k^2-1}{2}\right)^2 = k^2 + \frac{k^4 - 2k^2 + 1}{4} = \frac{k^4 + 2k^2 + 1}{4} = \left(\frac{k^2+1}{2}\right)^2$,
故$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$构成勾股数。
或证明法则(Ⅱ):
设$k$为大于2的偶数,则
$k^2 + \left(\left(\frac{k}{2}\right)^2 - 1\right)^2 = k^2 + \left(\frac{k^2}{4} - 1\right)^2 = \frac{k^4}{16} + \frac{k^2}{2} + 1 = \left(\left(\frac{k}{2}\right)^2 + 1\right)^2$,
故$k$,$\left(\frac{k}{2}\right)^2 - 1$,$\left(\frac{k}{2}\right)^2 + 1$构成勾股数。
答案:14. (1) 24;25
(2)
①
Ⅰ. 当$k=12$时,不满足法则(Ⅰ)($k$需为奇数),舍去;
法则(Ⅱ):
$k=12$,则
$\left(\frac{12}{2}\right)^2 - 1 = 35$,
$\left(\frac{12}{2}\right)^2 + 1 = 37$,
故另外两个数为35,37。
Ⅱ. 当$\frac{k^2-1}{2}=12$时,解得$k=5$($k$为奇数),
则$\frac{k^2+1}{2} = 13$,
故另外两个数为5,13。
综上,另外两个数为35,37或5,13。
②
证明法则(Ⅰ):
设$k$为大于1的奇数,则
$k^2 + \left(\frac{k^2-1}{2}\right)^2 = k^2 + \frac{k^4 - 2k^2 + 1}{4} = \frac{k^4 + 2k^2 + 1}{4} = \left(\frac{k^2+1}{2}\right)^2$,
故$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$构成勾股数。
或证明法则(Ⅱ):
设$k$为大于2的偶数,则
$k^2 + \left(\left(\frac{k}{2}\right)^2 - 1\right)^2 = k^2 + \left(\frac{k^2}{4} - 1\right)^2 = \frac{k^4}{16} + \frac{k^2}{2} + 1 = \left(\left(\frac{k}{2}\right)^2 + 1\right)^2$,
故$k$,$\left(\frac{k}{2}\right)^2 - 1$,$\left(\frac{k}{2}\right)^2 + 1$构成勾股数。
(2)
①
Ⅰ. 当$k=12$时,不满足法则(Ⅰ)($k$需为奇数),舍去;
法则(Ⅱ):
$k=12$,则
$\left(\frac{12}{2}\right)^2 - 1 = 35$,
$\left(\frac{12}{2}\right)^2 + 1 = 37$,
故另外两个数为35,37。
Ⅱ. 当$\frac{k^2-1}{2}=12$时,解得$k=5$($k$为奇数),
则$\frac{k^2+1}{2} = 13$,
故另外两个数为5,13。
综上,另外两个数为35,37或5,13。
②
证明法则(Ⅰ):
设$k$为大于1的奇数,则
$k^2 + \left(\frac{k^2-1}{2}\right)^2 = k^2 + \frac{k^4 - 2k^2 + 1}{4} = \frac{k^4 + 2k^2 + 1}{4} = \left(\frac{k^2+1}{2}\right)^2$,
故$k$,$\frac{k^2-1}{2}$,$\frac{k^2+1}{2}$构成勾股数。
或证明法则(Ⅱ):
设$k$为大于2的偶数,则
$k^2 + \left(\left(\frac{k}{2}\right)^2 - 1\right)^2 = k^2 + \left(\frac{k^2}{4} - 1\right)^2 = \frac{k^4}{16} + \frac{k^2}{2} + 1 = \left(\left(\frac{k}{2}\right)^2 + 1\right)^2$,
故$k$,$\left(\frac{k}{2}\right)^2 - 1$,$\left(\frac{k}{2}\right)^2 + 1$构成勾股数。