11. 一个长为120m、宽为100m的长方形场地要扩建成一个正方形场地,设长增加x m,宽增加y m,则y与x的函数表达式是
$y = x + 20$
,自变量的取值范围是$x \geq 0$
.答案:$y = x + 20$;$x \geq 0$。
解析:
由于扩建后的场地是正方形,所以扩建后的长和宽必须相等。
原场地的长为$120m$,增加的长度为$x m$,所以扩建后的长为$(120 + x)m$。
原场地的宽为$100m$,增加的宽度为$y m$,所以扩建后的宽为$(100 + y)m$
因此有:$120 + x = 100 + y$,
移项得:$y = x + 20$。
考虑实际扩建情况,长度和宽度增加的量都应为非负数值,即:$x \geq 0$,
同时,由于$y = x + 20$,且$y$代表宽度的增加量,也必须为非负数值,但这个条件已经由$x \geq 0$隐含,因为当$x \geq 0$时,$y = x + 20$必然大于0。
原场地的长为$120m$,增加的长度为$x m$,所以扩建后的长为$(120 + x)m$。
原场地的宽为$100m$,增加的宽度为$y m$,所以扩建后的宽为$(100 + y)m$
因此有:$120 + x = 100 + y$,
移项得:$y = x + 20$。
考虑实际扩建情况,长度和宽度增加的量都应为非负数值,即:$x \geq 0$,
同时,由于$y = x + 20$,且$y$代表宽度的增加量,也必须为非负数值,但这个条件已经由$x \geq 0$隐含,因为当$x \geq 0$时,$y = x + 20$必然大于0。
12. 已知一次函数$y= kx+b的图象与一次函数y= \frac{2-x}{3}$的图象互相平行,且与一次函数$y= -\frac{2x+1}{3}$的图象相交于y轴上同一点,则该一次函数的表达式为
$y = -\frac{1}{3}x - \frac{1}{3}$
.答案:该一次函数的表达式为$y = -\frac{1}{3}x - \frac{1}{3}$。(填答案时,只填$y = -\frac{1}{3}x - \frac{1}{3}$)
解析:
1. 由于一次函数$y = kx + b$的图象与一次函数$y = \frac{2 - x}{3}$的图象互相平行,根据平行直线的性质,斜率相等。因此,$k = -\frac{1}{3}$。
2. 一次函数$y = -\frac{2x + 1}{3}$与$y$轴的交点是当$x = 0$时的$y$值,计算得$y = -\frac{1}{3}$。
3. 由于一次函数$y = kx + b$的图象与一次函数$y = -\frac{2x + 1}{3}$的图象相交于$y$轴上同一点,因此$b = -\frac{1}{3}$。
4. 综合以上信息,该一次函数的表达式为$y = -\frac{1}{3}x - \frac{1}{3}$。
2. 一次函数$y = -\frac{2x + 1}{3}$与$y$轴的交点是当$x = 0$时的$y$值,计算得$y = -\frac{1}{3}$。
3. 由于一次函数$y = kx + b$的图象与一次函数$y = -\frac{2x + 1}{3}$的图象相交于$y$轴上同一点,因此$b = -\frac{1}{3}$。
4. 综合以上信息,该一次函数的表达式为$y = -\frac{1}{3}x - \frac{1}{3}$。
13. (12分)已知一次函数$y= (2m+4)x+(3-n)$.
(1) 当m,n满足什么条件时,y随x的增大而增大?
(2) 当m,n满足什么条件时,函数图象经过原点?
(3) 若函数图象经过第一、二、三象限,求m,n的取值范围.
(1) 当m,n满足什么条件时,y随x的增大而增大?
(2) 当m,n满足什么条件时,函数图象经过原点?
(3) 若函数图象经过第一、二、三象限,求m,n的取值范围.
答案:(1) 要使y随x的增大而增大,需要一次函数的斜率大于0。
即:$2m + 4 > 0$
解得:$m > -2$
n为任意实数,因为n不影响x的系数。
所以,当$m > -2$,n为任意实数时,y随x的增大而增大。
(2) 要使函数图象经过原点,即当$x=0$时,$y=0$。
将$x=0, y=0$代入$y = (2m + 4)x + (3 - n)$,得:
$0 = 3 - n$
解得:$n = 3$
同时,斜率$2m + 4$不能为0,即$m \neq -2$。
所以,当$m \neq -2$且$n = 3$时,函数图象经过原点。
(3) 要使函数图象经过第一、二、三象限,需要满足两个条件:
斜率$2m + 4 > 0$,即$m > -2$;
截距$3 - n > 0$,即$n < 3$。
所以,当$m > -2$且$n < 3$时,函数图象经过第一、二、三象限。
即:$2m + 4 > 0$
解得:$m > -2$
n为任意实数,因为n不影响x的系数。
所以,当$m > -2$,n为任意实数时,y随x的增大而增大。
(2) 要使函数图象经过原点,即当$x=0$时,$y=0$。
将$x=0, y=0$代入$y = (2m + 4)x + (3 - n)$,得:
$0 = 3 - n$
解得:$n = 3$
同时,斜率$2m + 4$不能为0,即$m \neq -2$。
所以,当$m \neq -2$且$n = 3$时,函数图象经过原点。
(3) 要使函数图象经过第一、二、三象限,需要满足两个条件:
斜率$2m + 4 > 0$,即$m > -2$;
截距$3 - n > 0$,即$n < 3$。
所以,当$m > -2$且$n < 3$时,函数图象经过第一、二、三象限。
14. (14分)如图,已知函数$y= -\frac{1}{2}x+b$的图象与x轴、y轴分别交于点A,B,与函数$y= x$的图象交于点M,点M的横坐标为2,在x轴上有一点$P(a,0)$(其中$a>2$),过点P作x轴的垂线,分别交函数$y= -\frac{1}{2}x+b和y= x$的图象于点C,D.
(1) 求点A的坐标;
(2) 若$CD= 3$,求a的值;
(3) 当$a= 5$时,求四边形OMCP的面积.
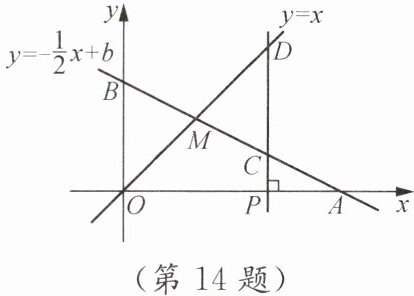
(1) 求点A的坐标;
(2) 若$CD= 3$,求a的值;
(3) 当$a= 5$时,求四边形OMCP的面积.

答案:(1) 因为点M是函数$y=-\frac{1}{2}x+b$与$y=x$的交点,且M的横坐标为2,将$x=2$代入$y=x$得$y=2$,所以$M(2,2)$。把$M(2,2)$代入$y=-\frac{1}{2}x+b$,得$2=-\frac{1}{2}×2+b$,解得$b=3$,则函数解析式为$y=-\frac{1}{2}x+3$。令$y=0$,得$0=-\frac{1}{2}x+3$,解得$x=6$,所以点A的坐标为$(6,0)$。
(2) 点P$(a,0)$,过P作x轴垂线$x=a$,交$y=-\frac{1}{2}x+3$于点C,交$y=x$于点D。则$C(a,-\frac{1}{2}a+3)$,$D(a,a)$。因为$a>2$,所以$CD=a-(-\frac{1}{2}a+3)=\frac{3}{2}a-3$。由$CD=3$得$\frac{3}{2}a-3=3$,解得$a=4$。
(3) 当$a=5$时,$P(5,0)$,$C(5,-\frac{1}{2}×5+3)=\left(5,\frac{1}{2}\right)$。过M作x轴垂线,垂足为$N(2,0)$。梯形$MNCP$的上底$MN=2$,下底$CP=\frac{1}{2}$,高$NP=5-2=3$,面积为$\frac{(2+\frac{1}{2})×3}{2}=\frac{15}{4}$。三角形$OMN$的面积为$\frac{1}{2}×2×2=2=\frac{8}{4}$。所以四边形$OMCP$的面积为$\frac{15}{4}+\frac{8}{4}=\frac{23}{4}$。
(1)$(6,0)$;(2)$4$;(3)$\frac{23}{4}$
(2) 点P$(a,0)$,过P作x轴垂线$x=a$,交$y=-\frac{1}{2}x+3$于点C,交$y=x$于点D。则$C(a,-\frac{1}{2}a+3)$,$D(a,a)$。因为$a>2$,所以$CD=a-(-\frac{1}{2}a+3)=\frac{3}{2}a-3$。由$CD=3$得$\frac{3}{2}a-3=3$,解得$a=4$。
(3) 当$a=5$时,$P(5,0)$,$C(5,-\frac{1}{2}×5+3)=\left(5,\frac{1}{2}\right)$。过M作x轴垂线,垂足为$N(2,0)$。梯形$MNCP$的上底$MN=2$,下底$CP=\frac{1}{2}$,高$NP=5-2=3$,面积为$\frac{(2+\frac{1}{2})×3}{2}=\frac{15}{4}$。三角形$OMN$的面积为$\frac{1}{2}×2×2=2=\frac{8}{4}$。所以四边形$OMCP$的面积为$\frac{15}{4}+\frac{8}{4}=\frac{23}{4}$。
(1)$(6,0)$;(2)$4$;(3)$\frac{23}{4}$
15. (14分)某块试验田的农作物每天的需水量y kg与生长时间x天之间的关系如图所示.这些农作物在第10天、第30天的需水量分别为2000 kg,3000 kg,在第40天后每天的需水量比前一天增加100 kg.
(1) 分别求出$x<40和x\geq40$时y关于x的函数表达式;
(2) 如果这些农作物每天的需水量大于或等于4000 kg时,就需要进行人工灌溉,那么应从第几天开始进行人工灌溉?

(1) 分别求出$x<40和x\geq40$时y关于x的函数表达式;
(2) 如果这些农作物每天的需水量大于或等于4000 kg时,就需要进行人工灌溉,那么应从第几天开始进行人工灌溉?

答案:(1) 当$x < 40$时,设$y = kx + b$。
把$(10, 2000)$,$(30, 3000)$代入得:
$\begin{cases}10k + b = 2000 \\30k + b = 3000 \end{cases}$
两式相减得$20k = 1000$,解得$k = 50$。
把$k = 50$代入$10k + b = 2000$,得$500 + b = 2000$,解得$b = 1500$。
所以$y = 50x + 1500(x < 40)$。
当$x\geq40$时,$x = 40$时,$y = 50×40 + 1500 = 3500$。
因为第$40$天后每天的需水量比前一天增加$100kg$,所以$y = 100(x - 40) + 3500 = 100x - 500(x\geq40)$。
(2) 当$y\geq4000$时,对于$y = 100x - 500(x\geq40)$,
有$100x - 500\geq4000$,
$100x\geq4500$,
解得$x\geq45$。
所以应从第$45$天开始进行人工灌溉。
把$(10, 2000)$,$(30, 3000)$代入得:
$\begin{cases}10k + b = 2000 \\30k + b = 3000 \end{cases}$
两式相减得$20k = 1000$,解得$k = 50$。
把$k = 50$代入$10k + b = 2000$,得$500 + b = 2000$,解得$b = 1500$。
所以$y = 50x + 1500(x < 40)$。
当$x\geq40$时,$x = 40$时,$y = 50×40 + 1500 = 3500$。
因为第$40$天后每天的需水量比前一天增加$100kg$,所以$y = 100(x - 40) + 3500 = 100x - 500(x\geq40)$。
(2) 当$y\geq4000$时,对于$y = 100x - 500(x\geq40)$,
有$100x - 500\geq4000$,
$100x\geq4500$,
解得$x\geq45$。
所以应从第$45$天开始进行人工灌溉。