1. 下列实数中,属于无理数的是(
A.-3
B.0
C.$\frac{2}{3}$
D.$\sqrt{5}$
D
)A.-3
B.0
C.$\frac{2}{3}$
D.$\sqrt{5}$
答案:D
解析:
无理数是指无限不循环小数,不能表示为两个整数的比。-3是整数,属于有理数;0也是整数,属于有理数;$\frac{2}{3}$是分数,属于有理数;$\sqrt{5}$是开方开不尽的数,是无限不循环小数,属于无理数。
2. 能判断两个三角形全等的条件是(
A.已知两角及一边相等
B.有两边及一角对应相等
C.已知三条边对应相等
D.有三个角对应相等
C
)A.已知两角及一边相等
B.有两边及一角对应相等
C.已知三条边对应相等
D.有三个角对应相等
答案:C
解析:
A. 已知两角及一边相等,这一条件可能是角角边(AAS)或角边角(ASA)的情况,这两种情况都可以判定两个三角形全等,但选项描述不够明确,因为它没有明确这条边是两角的夹边还是其中一角的对边,所以不能确定一定可以判定全等;B. 有两边及一角对应相等,这一条件可能是边边角(SSA)的情况,而边边角不能判定两个三角形全等;C. 已知三条边对应相等,这是边边边(SSS)的情况,根据三角形全等的判定定理,三边对应相等的两个三角形全等;D. 有三个角对应相等,这只能判定两个三角形相似,但不能判定它们全等。
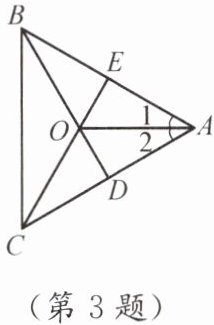
3. 如图,在AB,AC上分别取点E,D,使AE= AD,连接BD,CE,相交于点O,再连接AO,BC,若∠1= ∠2,则图中全等三角形共有(
A.5对
B.6对
C.7对
D.8对
C
)
A.5对
B.6对
C.7对
D.8对
答案:C
解析:
1. △AOE≌△AOD(SAS):AE=AD,∠1=∠2,AO=AO。
2. △BOE≌△COD(ASA):由1得OE=OD,∠AEO=∠ADO即∠BEO=∠CDO,∠BOE=∠COD(对顶角)。
3. △BOD≌△COE(SAS):由1得OD=OE,由2得OB=OC,∠BOD=∠COE(对顶角)。
4. △ABD≌△ACE(SAS):由2得BE=CD,结合AE=AD得AB=AC,AD=AE,∠BAD=∠CAE(公共角)。
5. △AOB≌△AOC(SSS):AB=AC,AO=AO,由2得OB=OC。
6. △ABE≌△ACD(SSS):AB=AC,AE=AD,由2得BE=CD。
7. △BEC≌△CDB(SSS):由2得BE=CD,BC=CB,由4得BD=CE。
2. △BOE≌△COD(ASA):由1得OE=OD,∠AEO=∠ADO即∠BEO=∠CDO,∠BOE=∠COD(对顶角)。
3. △BOD≌△COE(SAS):由1得OD=OE,由2得OB=OC,∠BOD=∠COE(对顶角)。
4. △ABD≌△ACE(SAS):由2得BE=CD,结合AE=AD得AB=AC,AD=AE,∠BAD=∠CAE(公共角)。
5. △AOB≌△AOC(SSS):AB=AC,AO=AO,由2得OB=OC。
6. △ABE≌△ACD(SSS):AB=AC,AE=AD,由2得BE=CD。
7. △BEC≌△CDB(SSS):由2得BE=CD,BC=CB,由4得BD=CE。
4. 如果一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为(
A.等边三角形
B.等腰直角三角形
C.直角三角形
D.钝角三角形
A
)A.等边三角形
B.等腰直角三角形
C.直角三角形
D.钝角三角形
答案:A
解析:
由题意知,三角形有两条边相等,所以它是等腰三角形。
若此三角形是含有一个角为$60^{\circ}$的等腰三角形,根据等腰三角形的性质:等腰三角形的两个底角相等,若底角为$60^{\circ}$,则另一个底角也为$60^{\circ}$,根据三角形内角和为$180^{\circ}$,则顶角也为$180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$;若顶角为$60^{\circ}$,则每个底角为$(180^{\circ}-60^{\circ})÷2=60^{\circ}$。
所以三个角都相等,根据等边三角形的判定:三个角都相等的三角形是等边三角形,可知这个三角形是等边三角形。
若此三角形是含有一个角为$60^{\circ}$的等腰三角形,根据等腰三角形的性质:等腰三角形的两个底角相等,若底角为$60^{\circ}$,则另一个底角也为$60^{\circ}$,根据三角形内角和为$180^{\circ}$,则顶角也为$180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$;若顶角为$60^{\circ}$,则每个底角为$(180^{\circ}-60^{\circ})÷2=60^{\circ}$。
所以三个角都相等,根据等边三角形的判定:三个角都相等的三角形是等边三角形,可知这个三角形是等边三角形。
5. 以下列各组数作为三角形的三条边长:①5,12,13;②9,40,41;③$\sqrt{2}$,$\sqrt{3}$,2;④15,25,20.其中,能构成直角三角形的有(
A.1组
B.2组
C.3组
D.4组
C
)A.1组
B.2组
C.3组
D.4组
答案:C
解析:
对于每一组数,分别验证是否满足勾股定理的逆定理(即$a^2 + b^2 = c^2$)来判断是否能构成直角三角形。
① 对于5,12,13:
$5^2 + 12^2 = 25 + 144 = 169 = 13^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
② 对于9,40,41:
$9^2 + 40^2 = 81 + 1600 = 1681 = 41^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
③ 对于$\sqrt{2}$,$\sqrt{3}$,2:
$(\sqrt{2})^2 + (\sqrt{3})^2 = 2 + 3 = 5 \neq 2^2=4$,
不满足勾股定理的逆定理,所以不能构成直角三角形。
④ 对于15,20,25:
$15^2 + 20^2 = 225 + 400 = 625 = 25^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
综上,能构成直角三角形的有3组。
① 对于5,12,13:
$5^2 + 12^2 = 25 + 144 = 169 = 13^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
② 对于9,40,41:
$9^2 + 40^2 = 81 + 1600 = 1681 = 41^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
③ 对于$\sqrt{2}$,$\sqrt{3}$,2:
$(\sqrt{2})^2 + (\sqrt{3})^2 = 2 + 3 = 5 \neq 2^2=4$,
不满足勾股定理的逆定理,所以不能构成直角三角形。
④ 对于15,20,25:
$15^2 + 20^2 = 225 + 400 = 625 = 25^2$,
满足勾股定理的逆定理,所以能构成直角三角形。
综上,能构成直角三角形的有3组。
6. 如图,在正方形网格中,网格线的交点称为格点.已知A,B是两个格点,如果C也是图中的格点,且使△ABC为等腰三角形,则满足条件的点C有(

A.9个
B.7个
C.5个
D.4个
A
)
A.9个
B.7个
C.5个
D.4个
答案:A
解析:
分三种情况讨论:
1. 以A为顶点,AB=AC:根据网格特点,找出与A距离等于AB的格点,共4个(除去B)。
2. 以B为顶点,BA=BC:同理,找出与B距离等于AB的格点,共4个(除去A)。
3. 以C为顶点,AC=BC:AB垂直平分线上的格点,共1个(不与A、B共线)。
综上,满足条件的点C共有4+4+1=9个。
1. 以A为顶点,AB=AC:根据网格特点,找出与A距离等于AB的格点,共4个(除去B)。
2. 以B为顶点,BA=BC:同理,找出与B距离等于AB的格点,共4个(除去A)。
3. 以C为顶点,AC=BC:AB垂直平分线上的格点,共1个(不与A、B共线)。
综上,满足条件的点C共有4+4+1=9个。
7. 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE……以此类推,则第n个等腰直角三角形斜边长的平方是(

A.2n
B.4n
C.$2^n$
D.$2^{2n}$
C
)
A.2n
B.4n
C.$2^n$
D.$2^{2n}$
答案:C
解析:
第1个等腰直角三角形△ABC,腰长为1,斜边长的平方为$1^2 + 1^2 = 2 = 2^1$;
第2个等腰直角三角形△ACD,直角边为第1个三角形的斜边,斜边长的平方为$2 + 2 = 4 = 2^2$;
第3个等腰直角三角形△ADE,直角边为第2个三角形的斜边,斜边长的平方为$4 + 4 = 8 = 2^3$;
...
以此类推,第n个等腰直角三角形斜边长的平方是$2^n$。
第2个等腰直角三角形△ACD,直角边为第1个三角形的斜边,斜边长的平方为$2 + 2 = 4 = 2^2$;
第3个等腰直角三角形△ADE,直角边为第2个三角形的斜边,斜边长的平方为$4 + 4 = 8 = 2^3$;
...
以此类推,第n个等腰直角三角形斜边长的平方是$2^n$。
8. $\sqrt{16}$的平方根是
$\pm 2$
.答案:由于本题为填空题,故直接填写结论,答案为$\pm 2$。
解析:
首先,根据平方根的定义,求出$\sqrt{16}$的值。
$\sqrt{16} = 4$
接着,要求出4的平方根。
根据平方根的性质,一个正数的平方根有两个值,一个正数和一个负数,即:
$\sqrt{4} = \pm 2$
所以,$\sqrt{16}$的平方根是$\pm 2$。
$\sqrt{16} = 4$
接着,要求出4的平方根。
根据平方根的性质,一个正数的平方根有两个值,一个正数和一个负数,即:
$\sqrt{4} = \pm 2$
所以,$\sqrt{16}$的平方根是$\pm 2$。