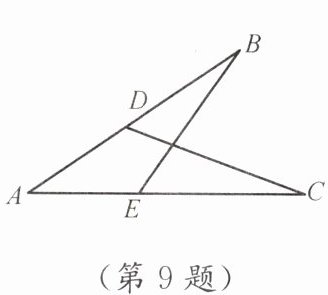
9. 如图,△ACD≌△ABE,AC= 8,CD= 7,AD= 3,则DB= ______.

5
答案:5
解析:
由于$\triangle ACD\cong\triangle ABE$,所以$AE=AC$,$AB=AD$。
已知$AC=8$,$AD=3$,则$AB=3$。
因此$DB=AC-AB=8-3=5$。
已知$AC=8$,$AD=3$,则$AB=3$。
因此$DB=AC-AB=8-3=5$。
10. 若等腰三角形的一个角是70°,则其底角为
70°或55°
.答案:由于本题为填空题,没有选项,故答案为$70^\circ$或$55^\circ$。
解析:
1. 当$70^\circ$角为底角时:
设等腰三角形的顶角为$\alpha$,则两个底角都是$70^\circ$。
根据三角形内角和为$180^\circ$,有$\alpha + 2 × 70^\circ = 180^\circ$。
解得$\alpha = 40^\circ$,这是一个合理的解,因为三角形的三个内角和为$180^\circ$。
2. 当$70^\circ$角为顶角时:
设等腰三角形的两个底角都为$\beta$。
根据三角形内角和为$180^\circ$,有$70^\circ + 2\beta = 180^\circ$。
解得$\beta = 55^\circ$,这也是一个合理的解。
综合以上两种情况,等腰三角形的底角可以是$70^\circ$或$55^\circ$。
设等腰三角形的顶角为$\alpha$,则两个底角都是$70^\circ$。
根据三角形内角和为$180^\circ$,有$\alpha + 2 × 70^\circ = 180^\circ$。
解得$\alpha = 40^\circ$,这是一个合理的解,因为三角形的三个内角和为$180^\circ$。
2. 当$70^\circ$角为顶角时:
设等腰三角形的两个底角都为$\beta$。
根据三角形内角和为$180^\circ$,有$70^\circ + 2\beta = 180^\circ$。
解得$\beta = 55^\circ$,这也是一个合理的解。
综合以上两种情况,等腰三角形的底角可以是$70^\circ$或$55^\circ$。
11. 如图,学校有一长方形花圃,有极少数人为了避开拐角而走“捷径”,在花圃内走出了一条“路”,其实他们仅仅少走了

4
m.
答案:4
解析:
1. 根据题意,少走的路程为原来需要走的路径长度减去“捷径”的长度。
2. 原来需要走的路径为长方形的两个边长之和,即 $8 + 6 = 14$ 米。
3. “捷径”为斜线,根据勾股定理,斜线的长度为 $\sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$ 米。
4. 少走的路程为 $14 - 10 = 4$ 米。
2. 原来需要走的路径为长方形的两个边长之和,即 $8 + 6 = 14$ 米。
3. “捷径”为斜线,根据勾股定理,斜线的长度为 $\sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$ 米。
4. 少走的路程为 $14 - 10 = 4$ 米。
12. 如图,点A,B在直线l的同侧,AB= 4,点C是点B关于直线l的对称点,AC交直线l于点D,AC= 5,则△ABD的周长为

9
.
答案:9
解析:
1. 根据题意,点$C$是点$B$关于直线$l$的对称点,因此$BD = CD$。
2. 由对称性可知,$AC = 5$,$AB = 4$。
3. 因为$D$是$AC$与直线$l$的交点,所以$AD$是$AC$的一部分。
4. 设$AD = x$,则$DC = 5 - x$。
5. 因为$BD = CD$,所以$BD = 5 - x$。
6. 在$\triangle ABD$中,$AB = 4$,$AD = x$,$BD = 5 - x$。
7. $\triangle ABD$的周长为$AB + AD + BD = 4 + x + (5 - x) = 9$。
2. 由对称性可知,$AC = 5$,$AB = 4$。
3. 因为$D$是$AC$与直线$l$的交点,所以$AD$是$AC$的一部分。
4. 设$AD = x$,则$DC = 5 - x$。
5. 因为$BD = CD$,所以$BD = 5 - x$。
6. 在$\triangle ABD$中,$AB = 4$,$AD = x$,$BD = 5 - x$。
7. $\triangle ABD$的周长为$AB + AD + BD = 4 + x + (5 - x) = 9$。
13. 如图,在△ABC中,∠C= 90°,DB平分∠ABC,E是AB的中点,DE⊥AB,若BC= 5,则AB=

10
.
答案:10
解析:
∵E是AB中点,DE⊥AB,∴DE垂直平分AB,∴DA=DB(线段垂直平分线上的点到两端距离相等),∴∠A=∠DBA。
∵DB平分∠ABC,∴∠DBA=∠DBC,设∠DBA=∠DBC=x,则∠ABC=2x,∠A=x。
在Rt△ABC中,∠C=90°,∴∠A+∠ABC=90°,即x+2x=90°,解得x=30°,∴∠A=30°。
∵∠A=30°,其对边为BC,∴BC=1/2AB(直角三角形中30°角所对直角边等于斜边一半),∵BC=5,∴AB=2BC=10。
∵DB平分∠ABC,∴∠DBA=∠DBC,设∠DBA=∠DBC=x,则∠ABC=2x,∠A=x。
在Rt△ABC中,∠C=90°,∴∠A+∠ABC=90°,即x+2x=90°,解得x=30°,∴∠A=30°。
∵∠A=30°,其对边为BC,∴BC=1/2AB(直角三角形中30°角所对直角边等于斜边一半),∵BC=5,∴AB=2BC=10。
14. 墙上钉了一根木条,小明想检验这根木条是否水平.他拿来一个如图所示的测平仪,在这个测平仪中,AB= AC,边BC的中点D处挂了一个重锤.小明将边BC与木条重合,观察此时重锤是否通过点A.如果重锤通过点A,那么这根木条是水平的,这是运用了

等腰三角形三线合一
的性质.
答案:等腰三角形三线合一
解析:
因为$AB=AC$,D为BC中点,根据等腰三角形三线合一的性质可知$AD\perp BC$,如果重锤通过点A,则说明木条与AD垂直,因为$AD\perp BC$,所以木条是水平的。
15. 如图,AD是△ABC的中线,且∠ADC= 60°,BC= 4.把△ADC沿直线AD折叠后,点C落在点C'的位置上,则BC'= ______.


2
答案:2
解析:
∵AD是△ABC的中线,BC=4,∴BD=DC=2。
∵△ADC沿AD折叠后点C落在C'处,∴DC'=DC=2,∠ADC'=∠ADC=60°。
∵D在BC上,∠ADC=60°,∴∠ADB=180°-∠ADC=120°。
∴∠BDC'=∠ADB-∠ADC'=120°-60°=60°。
在△BDC'中,BD=DC'=2,∠BDC'=60°,∴△BDC'是等边三角形。
∴BC'=BD=2。
∵△ADC沿AD折叠后点C落在C'处,∴DC'=DC=2,∠ADC'=∠ADC=60°。
∵D在BC上,∠ADC=60°,∴∠ADB=180°-∠ADC=120°。
∴∠BDC'=∠ADB-∠ADC'=120°-60°=60°。
在△BDC'中,BD=DC'=2,∠BDC'=60°,∴△BDC'是等边三角形。
∴BC'=BD=2。
16. 如图,圆柱形玻璃杯高为18 cm,底面周长为24 cm,在杯内壁离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁、离杯上沿2 cm且与蜂蜜相对的点A处,为了吃到蜂蜜,蚂蚁从外壁A处沿着最短路径爬到内壁B处,它爬行的最短距离是

20
cm.
答案:20
解析:
将圆柱形侧面展开为长24cm(底面周长)、宽18cm(高)的矩形。点B在离杯底4cm内壁,坐标为(0,4);点A在离上沿2cm外壁且与B相对,对称到内壁后坐标为(12,20)(水平距离12cm,垂直距离16cm)。最短路径为√(12²+16²)=20cm。
17. 如图,∠MAN是一钢架,且∠MAN= 10°,为了使钢架更加坚固,需在其内部添加一些钢管BC,CD,DE……若添加钢管的长度都与AB相等,则最多能添这样的钢管

4
根.
答案:4
解析:
∵∠MAN=10°,添加的钢管长度均与AB相等,即AB=BC=CD=DE=…,形成一系列等腰三角形。
在△ABC中,AB=BC,∴∠BAC=∠BCA=10°,外角∠CBD=∠BAC+∠BCA=20°;
在△BCD中,BC=CD,∴∠CBD=∠CDB=20°,外角∠DCE=∠CBD+∠CDB=40°;
在△CDE中,CD=DE,∴∠DCE=∠DEC=40°,外角∠EDF=∠DCE+∠DEC=80°;
在△DEF中,DE=EF,∴∠EDF=∠EFD=80°,外角∠FEG=∠EDF+∠EFD=160°;
下一个等腰三角形底角为160°,两底角和>180°,无法构成三角形。
共添加BC、CD、DE、EF四根钢管。
在△ABC中,AB=BC,∴∠BAC=∠BCA=10°,外角∠CBD=∠BAC+∠BCA=20°;
在△BCD中,BC=CD,∴∠CBD=∠CDB=20°,外角∠DCE=∠CBD+∠CDB=40°;
在△CDE中,CD=DE,∴∠DCE=∠DEC=40°,外角∠EDF=∠DCE+∠DEC=80°;
在△DEF中,DE=EF,∴∠EDF=∠EFD=80°,外角∠FEG=∠EDF+∠EFD=160°;
下一个等腰三角形底角为160°,两底角和>180°,无法构成三角形。
共添加BC、CD、DE、EF四根钢管。