2. 如图,在△ABC 中,AD⊥BC,D 是 BC 的中点,DE⊥AB,DF⊥AC,垂足分别为 E,F,图中的全等三角形共有(
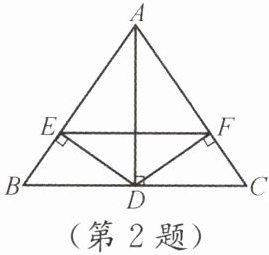
A.5 对
B.4 对
C.3 对
D.2 对
B
)
A.5 对
B.4 对
C.3 对
D.2 对
答案:B
解析:
点D是BC的中点,所以$BD=DC$。
$AD\perp BC$,所以$\angle ADB=\angle ADC=90^\circ$。
在$\triangle ADB$和$\triangle ADC$中:
$BD=DC$,$\angle ADB=\angle ADC$,$AD=AD$。
所以$\triangle ADB\cong\triangle ADC$(SAS)。
$DE\perp AB$,$DF\perp AC$,所以$\angle BED=\angle CFD=90^\circ$。
因为$\triangle ADB\cong\triangle ADC$,所以$\angle B=\angle C$,$AB=AC$。
在$\triangle BDE$和$\triangle CDF$中:
$\angle BED=\angle CFD$,$\angle B=\angle C$,$BD=DC$。
所以$\triangle BDE\cong\triangle CDF$(AAS)。
$DE=DF$(全等三角形对应边相等)。
在$\triangle ADE$和$\triangle ADF$中:
$\angle AED=\angle AFD=90^\circ$,$AD=AD$,$DE=DF$。
所以$\triangle ADE\cong\triangle ADF$(HL)。
$AE=AF$(全等三角形对应边相等)。
在$\triangle ABF$和$\triangle ACE$中:
$\angle BAF=\angle CAE$,$AB=AC$,$AF=AE$。
所以$\triangle ABF\cong\triangle ACE$(SAS)。
所以全等三角形共有4对。
$AD\perp BC$,所以$\angle ADB=\angle ADC=90^\circ$。
在$\triangle ADB$和$\triangle ADC$中:
$BD=DC$,$\angle ADB=\angle ADC$,$AD=AD$。
所以$\triangle ADB\cong\triangle ADC$(SAS)。
$DE\perp AB$,$DF\perp AC$,所以$\angle BED=\angle CFD=90^\circ$。
因为$\triangle ADB\cong\triangle ADC$,所以$\angle B=\angle C$,$AB=AC$。
在$\triangle BDE$和$\triangle CDF$中:
$\angle BED=\angle CFD$,$\angle B=\angle C$,$BD=DC$。
所以$\triangle BDE\cong\triangle CDF$(AAS)。
$DE=DF$(全等三角形对应边相等)。
在$\triangle ADE$和$\triangle ADF$中:
$\angle AED=\angle AFD=90^\circ$,$AD=AD$,$DE=DF$。
所以$\triangle ADE\cong\triangle ADF$(HL)。
$AE=AF$(全等三角形对应边相等)。
在$\triangle ABF$和$\triangle ACE$中:
$\angle BAF=\angle CAE$,$AB=AC$,$AF=AE$。
所以$\triangle ABF\cong\triangle ACE$(SAS)。
所以全等三角形共有4对。
3. 已知:如图,点 D 在 AB 上,点 E 在 AC 上,∠B= ∠C,BE 与 CD 相交于点 O,AB= AC. 求证:△DOB≌△EOC.


答案:在△ABE和△ACD中,
∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴△ABE≌△ACD(ASA),
∴AD=AE(全等三角形对应边相等),
∵AB=AC,
∴AB-AD=AC-AE,即BD=CE,
在△DOB和△EOC中,
∠B=∠C(已知),
∠DOB=∠EOC(对顶角相等),
BD=CE(已证),
∴△DOB≌△EOC(AAS)。
∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴△ABE≌△ACD(ASA),
∴AD=AE(全等三角形对应边相等),
∵AB=AC,
∴AB-AD=AC-AE,即BD=CE,
在△DOB和△EOC中,
∠B=∠C(已知),
∠DOB=∠EOC(对顶角相等),
BD=CE(已证),
∴△DOB≌△EOC(AAS)。
4. 如图,点 A,D,C,B 在同一条直线上,AD= BC,AE= BF,CE= DF.
(1)求证:△BFD≌△AEC.
(2)求证:DE= CF.

(1)求证:△BFD≌△AEC.
(2)求证:DE= CF.

答案:(1)
因为$AD = BC$,所以$AD + DC=BC + DC$,即$AC = BD$。
在$\triangle BFD$和$\triangle AEC$中,$\begin{cases}AC = BD\\AE = BF\\CE = DF\end{cases}$
根据$SSS$(边边边)全等判定定理,可得$\triangle BFD\cong\triangle AEC$。
(2)
由(1)知$\triangle BFD\cong\triangle AEC$,根据全等三角形的性质,全等三角形的对应边相等,所以$DE = CF$。
因为$AD = BC$,所以$AD + DC=BC + DC$,即$AC = BD$。
在$\triangle BFD$和$\triangle AEC$中,$\begin{cases}AC = BD\\AE = BF\\CE = DF\end{cases}$
根据$SSS$(边边边)全等判定定理,可得$\triangle BFD\cong\triangle AEC$。
(2)
由(1)知$\triangle BFD\cong\triangle AEC$,根据全等三角形的性质,全等三角形的对应边相等,所以$DE = CF$。
如图,在△ABC 中,AB= AC,且 AB>BC. 点 D 在边 BC 上,点 E,F 在线段 AD 上. ∠1,∠2 分别是△ABE,△CAF 的外角,且∠1= ∠2= ∠BAC.
(1)求证:△ABE≌△CAF;
(2)若 CD= 2BD,△ABC 的面积为 12,则△ABE 与△CDF 的面积之和为______
(1)求证:△ABE≌△CAF;
(2)若 CD= 2BD,△ABC 的面积为 12,则△ABE 与△CDF 的面积之和为______
8
$.zyjl.cn/pic18/2025-09-04/429a79429850ca3b4cdc0ae6f41565a3.jpg?x-oss-process=image/crop,x_1502,y_1960,w_256,h_308">$答案:(1) 证明:
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠BAE+∠ABE=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
$\left\{\begin{matrix}\angle ABE=\angle CAF,\\AB=CA,\\\angle BAE=\angle ACF.\end{matrix}\right.$
∴△ABE≌△CAF(ASA)。
(2) ∵△ABE≌△CAF,
∴$S_{△ABE}=S_{△CAF}$,
∴$S_{△ABE}+S_{△CDF}=S_{△CAF}+S_{△CDF}=S_{△ACD}$,
∵$CD=2BD$,
∴$BC=3BD$,
∵$AB=AC$,
∴$S_{△ABC}=3S_{△ABD}$,
∵$S_{△ABC}=12$,
∴$S_{△ABD}=4$,
∴$S_{△ACD}=2S_{△ABD}=8$,
∴$S_{△ABE}+S_{△CDF}=8$。
因此,答案为8。
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠BAE+∠ABE=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
$\left\{\begin{matrix}\angle ABE=\angle CAF,\\AB=CA,\\\angle BAE=\angle ACF.\end{matrix}\right.$
∴△ABE≌△CAF(ASA)。
(2) ∵△ABE≌△CAF,
∴$S_{△ABE}=S_{△CAF}$,
∴$S_{△ABE}+S_{△CDF}=S_{△CAF}+S_{△CDF}=S_{△ACD}$,
∵$CD=2BD$,
∴$BC=3BD$,
∵$AB=AC$,
∴$S_{△ABC}=3S_{△ABD}$,
∵$S_{△ABC}=12$,
∴$S_{△ABD}=4$,
∴$S_{△ACD}=2S_{△ABD}=8$,
∴$S_{△ABE}+S_{△CDF}=8$。
因此,答案为8。