活动一:想一想 说一说
(1)等腰三角形的定义是
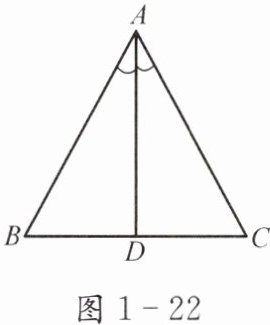
(2)如图1-22,把等腰三角形纸片ABC沿边BC的中线AD折叠,你有什么发现?
(3)通过第(2)题的探究,你能得到等腰三角形有哪些性质?
(4)证明上述得到的结论.
(1)等腰三角形的定义是
有两边相等的三角形叫做等腰三角形
.(2)如图1-22,把等腰三角形纸片ABC沿边BC的中线AD折叠,你有什么发现?

(3)通过第(2)题的探究,你能得到等腰三角形有哪些性质?
(4)证明上述得到的结论.
答案:按照上述解析内容进行理解
解析:
(1)等腰三角形的定义是有两边相等的三角形叫做等腰三角形。
(2)把等腰三角形纸片$ABC$沿边$BC$的中线$AD$折叠,发现$AB$与$AC$重合,$BD$与$CD$重合,$\angle B$与$\angle C$重合,$\angle BAD$与$\angle CAD$重合。
(3)通过第
(2)题的探究,能得到等腰三角形的性质:等腰三角形的两个底角相等;等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合(三线合一)。
(4)证明等腰三角形的两个底角相等:
已知:在$\triangle ABC$中,$AB = AC$。
求证:$\angle B=\angle C$。
证明:取$BC$中点$D$,连接$AD$。
因为$AB = AC$,$BD = CD$,$AD = AD$,
所以$\triangle ABD\cong\triangle ACD(SSS)$,
所以$\angle B=\angle C$。
证明等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合:
已知:在$\triangle ABC$中,$AB = AC$,$AD$平分$\angle BAC$,交$BC$于点$D$。
求证:$AD$是$BC$边上的中线,$AD$是$BC$边上的高。
证明:因为$AD$平分$\angle BAC$,所以$\angle BAD=\angle CAD$。
又因为$AB = AC$,$AD = AD$,
所以$\triangle ABD\cong\triangle ACD(SAS)$,
所以$BD = CD$,$\angle ADB=\angle ADC$。
因为$\angle ADB+\angle ADC = 180^{\circ}$,所以$\angle ADB=\angle ADC = 90^{\circ}$,
即$AD\perp BC$。
|文字语言|图形语言|符号语言|
|等边对等角||在△ABC中,
因为AB= AC,
所以
|底边上的高、
中线及顶角
平分线重合||在△ABC中,AB= AC.
(1)因为∠BAD= ∠CAD,所以
(2)因为AD⊥BC,所以
(3)因为BD= CD,所以

|等边对等角||在△ABC中,
因为AB= AC,
所以
∠B
=∠C
.||底边上的高、
中线及顶角
平分线重合||在△ABC中,AB= AC.
(1)因为∠BAD= ∠CAD,所以
△ABD≌△ACD(ASA),BD = CD
;(2)因为AD⊥BC,所以
∠BAD=∠CAD,BD = CD
;(3)因为BD= CD,所以
∠BAD=∠CAD,AD⊥BC
.|
答案:
$\angle B$;$\angle C$;
$\triangle ABD\cong\triangle ACD(ASA)$,$BD = CD$;$\angle BAD=\angle CAD$,$BD = CD$;$\angle BAD=\angle CAD$,$AD\perp BC$。
$\angle B$;$\angle C$;
$\triangle ABD\cong\triangle ACD(ASA)$,$BD = CD$;$\angle BAD=\angle CAD$,$BD = CD$;$\angle BAD=\angle CAD$,$AD\perp BC$。
解析:
对于等腰三角形,等边对等角,所以在$\triangle ABC$中,由于$AB = AC$,那么$\angle B=\angle C$。
在等腰$\triangle ABC$中,$AB = AC$:
(1)当$\angle BAD=\angle CAD$时,根据等腰三角形三线合一的性质(顶角的平分线、底边上的中线、底边上的高互相重合),可知$AD$是顶角平分线,所以$AD\perp BC$,$BD = CD$,即$\triangle ABD\cong\triangle ACD(ASA)$,所以$BD=CD$。
(2)当$AD\perp BC$时,因为等腰三角形三线合一,所以$AD$是底边上的高,同时也是顶角平分线和底边中线,可得$\angle BAD=\angle CAD$,$BD = CD$。
(3)当$BD = CD$时,由于等腰三角形三线合一,所以$AD$是底边中线,同时也是顶角平分线和底边上的高,即$\angle BAD=\angle CAD$,$AD\perp BC$。