1. 在△ABC中,AB= AC.
(1)已知∠A= 70°,则∠C=
(2)已知∠B= 30°,则∠A=
(3)已知有一个角等于55°,则其余两个角分别是
(1)已知∠A= 70°,则∠C=
55°
,∠B= 55°
;(2)已知∠B= 30°,则∠A=
120°
,∠C= 30°
;(3)已知有一个角等于55°,则其余两个角分别是
55°,70°;或62.5°,62.5°
.答案:[分析]
根据等腰三角形的性质,两个底角相等,利用三角形内角和定理(三角形三个内角的和等于$180^{\circ}$)求解即可。
[解答]
(1)已知$\angle A=70^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C$(等腰三角形两底角相等)
因为三角形内角和为$180^{\circ}$
所以$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-70^{\circ}}{2}=55^{\circ}$
答案为:$55^{\circ}$;$55^{\circ}$
(2)已知$\angle B=30^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=30^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$
答案为:$120^{\circ}$;$30^{\circ}$
(3)已知一个角等于$55^{\circ}$
若$\angle A=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C$(等腰三角形两底角相等)
所以$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-55^{\circ}}{2}=62.5^{\circ}$
若$\angle B=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=55^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-55^{\circ}=70^{\circ}$
若$\angle C=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=55^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-55^{\circ}=70^{\circ}$
答案为:$55^{\circ}$,$70^{\circ}$;或$62.5^{\circ}$,$62.5^{\circ}$
[总结]
通过对等腰三角形性质和三角形内角和定理的运用,逐步推导出各个角的度数。
[答案]
(1)$55^{\circ}$;$55^{\circ}$
(2)$120^{\circ}$;$30^{\circ}$
(3)$55^{\circ}$,$70^{\circ}$;或$62.5^{\circ}$,$62.5^{\circ}$
根据等腰三角形的性质,两个底角相等,利用三角形内角和定理(三角形三个内角的和等于$180^{\circ}$)求解即可。
[解答]
(1)已知$\angle A=70^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C$(等腰三角形两底角相等)
因为三角形内角和为$180^{\circ}$
所以$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-70^{\circ}}{2}=55^{\circ}$
答案为:$55^{\circ}$;$55^{\circ}$
(2)已知$\angle B=30^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=30^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$
答案为:$120^{\circ}$;$30^{\circ}$
(3)已知一个角等于$55^{\circ}$
若$\angle A=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C$(等腰三角形两底角相等)
所以$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-55^{\circ}}{2}=62.5^{\circ}$
若$\angle B=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=55^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-55^{\circ}=70^{\circ}$
若$\angle C=55^{\circ}$
因为$AB=AC$
所以$\angle B=\angle C=55^{\circ}$(等腰三角形两底角相等)
所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-55^{\circ}-55^{\circ}=70^{\circ}$
答案为:$55^{\circ}$,$70^{\circ}$;或$62.5^{\circ}$,$62.5^{\circ}$
[总结]
通过对等腰三角形性质和三角形内角和定理的运用,逐步推导出各个角的度数。
[答案]
(1)$55^{\circ}$;$55^{\circ}$
(2)$120^{\circ}$;$30^{\circ}$
(3)$55^{\circ}$,$70^{\circ}$;或$62.5^{\circ}$,$62.5^{\circ}$
解析:
(1)∵AB=AC,∴∠B=∠C,∵∠A=70°,∠A+∠B+∠C=180°,∴∠B=∠C=(180°-70°)÷2=55°;
(2)∵AB=AC,∴∠B=∠C=30°,∵∠A+∠B+∠C=180°,∴∠A=180°-30°-30°=120°;
(3)当55°角为顶角时,底角=(180°-55°)÷2=62.5°,其余两角为62.5°,62.5°;当55°角为底角时,顶角=180°-55°×2=70°,其余两角为55°,70°。
(2)∵AB=AC,∴∠B=∠C=30°,∵∠A+∠B+∠C=180°,∴∠A=180°-30°-30°=120°;
(3)当55°角为顶角时,底角=(180°-55°)÷2=62.5°,其余两角为62.5°,62.5°;当55°角为底角时,顶角=180°-55°×2=70°,其余两角为55°,70°。
2. 选择题:
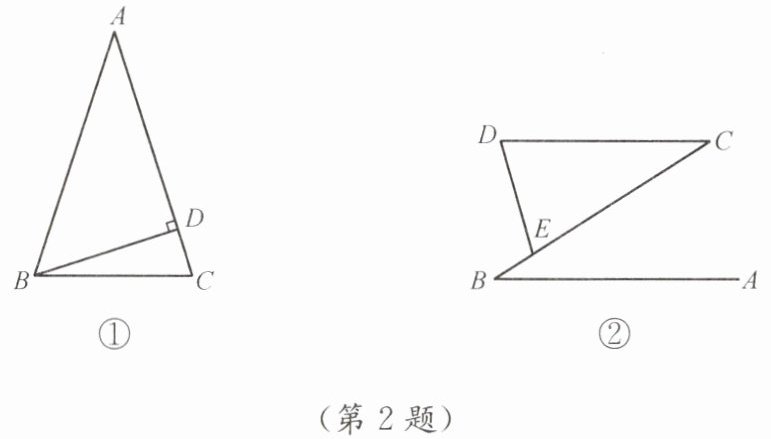
(1)如图①,在△ABC中,AB= AC,∠A= 36°,BD是边AC上的高,则∠DBC的度数是(
A. 18°
B. 24°
C. 30°
D. 36°
(2)等腰三角形的一边长为10,另一边长为7,它的周长是(
A. 27
B. 24
C. 17
D. 27或24
(3)如图②,AB//CD,点E在BC上,且CD= CE,∠D= 74°,则∠B的度数是(
A. 68°
B. 32°
C. 22°
D. 16°
(1)如图①,在△ABC中,AB= AC,∠A= 36°,BD是边AC上的高,则∠DBC的度数是(
A
)A. 18°
B. 24°
C. 30°
D. 36°

(2)等腰三角形的一边长为10,另一边长为7,它的周长是(
D
)A. 27
B. 24
C. 17
D. 27或24
(3)如图②,AB//CD,点E在BC上,且CD= CE,∠D= 74°,则∠B的度数是(
B
)A. 68°
B. 32°
C. 22°
D. 16°
答案:(1)A
(2)D
(3)B
(2)D
(3)B
解析:
(1)在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,根据等腰三角形两底角相等及三角形内角和为$180^{\circ}$,可得$\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180 - 36}{2}=72^{\circ}$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$,在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90 - 72 = 18^{\circ}$。
(2)分两种情况讨论:
当等腰三角形的腰长为$10$,底边长为$7$时,根据三角形三边关系(任意两边之和大于第三边),$10 + 10>7$,$10 + 7>10$,能构成三角形,此时周长为$10 + 10 + 7 = 27$。
当等腰三角形的腰长为$7$,底边长为$10$时,$7 + 7>10$,$7 + 10>7$,能构成三角形,此时周长为$7 + 7 + 10 = 24$。
所以它的周长是$27$或$24$。
(3)因为$CD = CE$,所以$\angle DEC=\angle D = 74^{\circ}$。
根据邻补角的性质,$\angle C = 180^{\circ}-2×74^{\circ}=180 - 148 = 32^{\circ}$。
又因为$AB// CD$,根据两直线平行,同位角相等,所以$\angle B=\angle C = 32^{\circ}$。
因为$BD$是边$AC$上的高,所以$\angle BDC = 90^{\circ}$,在$\triangle BDC$中,$\angle DBC=180^{\circ}-\angle BDC-\angle C=180 - 90 - 72 = 18^{\circ}$。
(2)分两种情况讨论:
当等腰三角形的腰长为$10$,底边长为$7$时,根据三角形三边关系(任意两边之和大于第三边),$10 + 10>7$,$10 + 7>10$,能构成三角形,此时周长为$10 + 10 + 7 = 27$。
当等腰三角形的腰长为$7$,底边长为$10$时,$7 + 7>10$,$7 + 10>7$,能构成三角形,此时周长为$7 + 7 + 10 = 24$。
所以它的周长是$27$或$24$。
(3)因为$CD = CE$,所以$\angle DEC=\angle D = 74^{\circ}$。
根据邻补角的性质,$\angle C = 180^{\circ}-2×74^{\circ}=180 - 148 = 32^{\circ}$。
又因为$AB// CD$,根据两直线平行,同位角相等,所以$\angle B=\angle C = 32^{\circ}$。
3. 如图,在△ABC中,AB= AC,AD⊥BC,点E在CA的延长线上,AE= AF. 试判断EF与AD的位置关系,并说明理由.


答案:EF与AD平行。理由如下:
∵AB=AC,∴△ABC是等腰三角形,∠B=∠C。
∵AD⊥BC,∴AD平分∠BAC(等腰三角形三线合一),即∠CAD=∠BAC/2。
∵E在CA延长线上,AE=AF,∴△AEF是等腰三角形,∠E=∠AFE。
在△AEF中,∠EAF+∠E+∠AFE=180°,∴∠EAF=180°-2∠E。
∵C、A、E共线,∴∠EAF=180°-∠BAC(邻补角定义)。
∴180°-∠BAC=180°-2∠E,即∠BAC=2∠E,∴∠E=∠BAC/2。
∵∠CAD=∠BAC/2,∴∠E=∠CAD。
∴EF//AD(内错角相等,两直线平行)。
结论:EF//AD。
∵AB=AC,∴△ABC是等腰三角形,∠B=∠C。
∵AD⊥BC,∴AD平分∠BAC(等腰三角形三线合一),即∠CAD=∠BAC/2。
∵E在CA延长线上,AE=AF,∴△AEF是等腰三角形,∠E=∠AFE。
在△AEF中,∠EAF+∠E+∠AFE=180°,∴∠EAF=180°-2∠E。
∵C、A、E共线,∴∠EAF=180°-∠BAC(邻补角定义)。
∴180°-∠BAC=180°-2∠E,即∠BAC=2∠E,∴∠E=∠BAC/2。
∵∠CAD=∠BAC/2,∴∠E=∠CAD。
∴EF//AD(内错角相等,两直线平行)。
结论:EF//AD。
1. 填空题:
(1)若等腰三角形的一个外角为70°,则它的底角为
(2)如图,AB= AC,BD= BC,∠A= 40°,则∠ABD=

(3)已知等腰三角形一腰上的中线把三角形的周长分为12和15两部分,则它的底边长是
(1)若等腰三角形的一个外角为70°,则它的底角为
35°
;(2)如图,AB= AC,BD= BC,∠A= 40°,则∠ABD=
30°
;
(3)已知等腰三角形一腰上的中线把三角形的周长分为12和15两部分,则它的底边长是
7或11
.答案:(1)35°;(2)30°;(3)7或11
解析:
(1)等腰三角形外角为70°,则内角为110°,110°只能为顶角,底角=(180°-110°)/2=35°;(2)AB=AC,∠A=40°,∠ABC=∠ACB=70°,BD=BC,∠BDC=∠ACB=70°,∠DBC=40°,∠ABD=70°-40°=30°;(3)设腰长2x,底y,中线分周长为3x和x+y。若3x=12,x=4,y=15-4=11;若3x=15,x=5,y=12-5=7,均符合三边关系,底边长7或11。