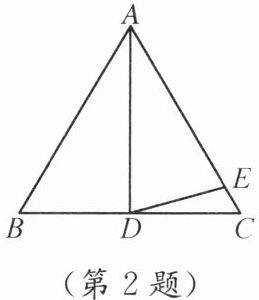
2. 如图,在△ABC中,AB= BC= AC,AD 是中线,点 E 在边 AC 上,AE= AD,则∠EDC= ______°.

15
答案:15
解析:
∵AB=BC=AC,∴△ABC是等边三角形,∠BAC=∠C=60°。
∵AD是中线,∴AD平分∠BAC,AD⊥BC(三线合一),∴∠CAD=30°,∠ADC=90°。
∵AE=AD,∴△ADE是等腰三角形,∠ADE=∠AED。
在△ADE中,∠DAE=30°,∴∠ADE=(180°-30°)/2=75°。
∵∠ADC=∠ADE+∠EDC=90°,∴∠EDC=90°-75°=15°。
∵AD是中线,∴AD平分∠BAC,AD⊥BC(三线合一),∴∠CAD=30°,∠ADC=90°。
∵AE=AD,∴△ADE是等腰三角形,∠ADE=∠AED。
在△ADE中,∠DAE=30°,∴∠ADE=(180°-30°)/2=75°。
∵∠ADC=∠ADE+∠EDC=90°,∴∠EDC=90°-75°=15°。
3. 以正方形 ABCD 的一边 CD 为边向外作等边三角形 CDE,则∠AEB=

30
°.
答案:30
解析:
设正方形ABCD边长为a,等边三角形CDE中CD=CE=DE=a,∠CDE=∠DCE=60°。
在正方形ABCD中,AD=CD=a,∠ADC=90°,故AD=DE,△ADE为等腰三角形。∠ADE=∠ADC+∠CDE=90°+60°=150°(或由几何关系得150°),则∠DAE=(180°-150°)/2=15°。
同理,BC=CD=CE=a,∠BCE=90°+60°=150°,△BCE为等腰三角形,∠CBE=15°。
在△AEB中,∠EAB=∠DAB-∠DAE=90°-15°=75°,∠EBA=∠CBA-∠CBE=90°-15°=75°,故∠AEB=180°-75°-75°=30°。
在正方形ABCD中,AD=CD=a,∠ADC=90°,故AD=DE,△ADE为等腰三角形。∠ADE=∠ADC+∠CDE=90°+60°=150°(或由几何关系得150°),则∠DAE=(180°-150°)/2=15°。
同理,BC=CD=CE=a,∠BCE=90°+60°=150°,△BCE为等腰三角形,∠CBE=15°。
在△AEB中,∠EAB=∠DAB-∠DAE=90°-15°=75°,∠EBA=∠CBA-∠CBE=90°-15°=75°,故∠AEB=180°-75°-75°=30°。
4. 如图,在△ABC中,AB= AC,∠BAC= 120°,AD⊥AB,AE⊥AC,垂足均为 A.△ADE 是等边三角形吗? 为什么?


答案:△ADE是等边三角形。理由如下:
∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)/2=(180°-120°)/2=30°。
∵AD⊥AB,
∴∠BAD=90°,
∴∠ADB=180°-∠BAD-∠B=180°-90°-30°=60°。
∵AE⊥AC,
∴∠CAE=90°,
∴∠AEC=180°-∠CAE-∠C=180°-90°-30°=60°。
∵∠DAE=∠BAD+∠CAE-∠BAC=90°+90°-120°=60°,
在△ADE中,∠DAE=60°,∠ADE=∠ADB=60°,∠AED=∠AEC=60°,
∴∠DAE=∠ADE=∠AED=60°,
∴△ADE是等边三角形。
∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)/2=(180°-120°)/2=30°。
∵AD⊥AB,
∴∠BAD=90°,
∴∠ADB=180°-∠BAD-∠B=180°-90°-30°=60°。
∵AE⊥AC,
∴∠CAE=90°,
∴∠AEC=180°-∠CAE-∠C=180°-90°-30°=60°。
∵∠DAE=∠BAD+∠CAE-∠BAC=90°+90°-120°=60°,
在△ADE中,∠DAE=60°,∠ADE=∠ADB=60°,∠AED=∠AEC=60°,
∴∠DAE=∠ADE=∠AED=60°,
∴△ADE是等边三角形。
5. 如图,AB= BC,∠CDE= 120°,DF//BA,且 DF 平分∠CDE.求证:△ABC 是等边三角形.


答案:∵∠CDE=120°,DF平分∠CDE,
∴∠FDC=∠CDE/2=60°(角平分线定义)。
∵D、B、C在同一直线上,
∴∠FDB=∠FDC=60°。
∵DF//BA,
∴∠ABD=∠FDB=60°(两直线平行,内错角相等)。
∵∠ABD=∠ABC,
∴∠ABC=60°。
∵AB=BC,
∴△ABC是等腰三角形,且顶角∠ABC=60°,
∴△ABC是等边三角形(有一个角为60°的等腰三角形是等边三角形)。
∴∠FDC=∠CDE/2=60°(角平分线定义)。
∵D、B、C在同一直线上,
∴∠FDB=∠FDC=60°。
∵DF//BA,
∴∠ABD=∠FDB=60°(两直线平行,内错角相等)。
∵∠ABD=∠ABC,
∴∠ABC=60°。
∵AB=BC,
∴△ABC是等腰三角形,且顶角∠ABC=60°,
∴△ABC是等边三角形(有一个角为60°的等腰三角形是等边三角形)。
1. 等腰三角形的周长为 80,若以它的底边为边的等边三角形的周长为 30,则该等腰三角形的腰长为(
A.25
B.35
C.30
D.40
B
)A.25
B.35
C.30
D.40
答案:B
解析:
以底边为边的等边三角形周长为30,则底边长为30÷3=10。等腰三角形周长为80,腰长=(80-10)÷2=35。
2. 如图,在等边三角形 ABC 中,D 是 AC 的中点,E 是 BC 延长线上的一点,且 CE= CD,DM⊥BC,垂足为 M.求证:M 是 BE 的中点.


答案:证明:
连接$BD$。
$\because$在等边$\triangle ABC$中,且$D$是$AC$的中点,
$\therefore \angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×60^{\circ}=30^{\circ}$,$\angle ACB=60^{\circ}$,
$\because CD = CE$,
$\therefore \angle CDE=\angle E$,
$\because \angle ACB=\angle CDE+\angle E=60^{\circ}$,
$\therefore \angle E=30^{\circ}$,
$\therefore \angle DBC=\angle E=30^{\circ}$,
$\because DM\perp BC$,即$\angle DMB=\angle DME=90^{\circ}$,
在$\triangle BDM$和$\triangle EDM$中,
$\begin{cases}\angle DBC=\angle E,\\ DM=DM,\\\angle DMB=\angle DME.\end{cases}$
$\therefore \triangle BDM\cong\triangle EDM(ASA)$,
$\therefore BM = EM$,
即$M$是$BE$的中点。
连接$BD$。
$\because$在等边$\triangle ABC$中,且$D$是$AC$的中点,
$\therefore \angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×60^{\circ}=30^{\circ}$,$\angle ACB=60^{\circ}$,
$\because CD = CE$,
$\therefore \angle CDE=\angle E$,
$\because \angle ACB=\angle CDE+\angle E=60^{\circ}$,
$\therefore \angle E=30^{\circ}$,
$\therefore \angle DBC=\angle E=30^{\circ}$,
$\because DM\perp BC$,即$\angle DMB=\angle DME=90^{\circ}$,
在$\triangle BDM$和$\triangle EDM$中,
$\begin{cases}\angle DBC=\angle E,\\ DM=DM,\\\angle DMB=\angle DME.\end{cases}$
$\therefore \triangle BDM\cong\triangle EDM(ASA)$,
$\therefore BM = EM$,
即$M$是$BE$的中点。