活动三:想一想 做一做
1. 感受化归思想.
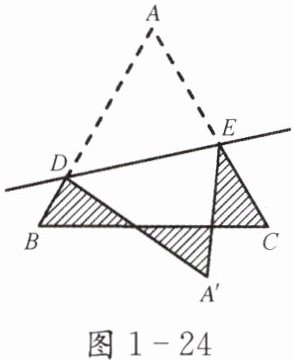
如图1-24,等边三角形ABC的边长为1,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC的外部,则阴影部分的周长为
2. 感受分类思想.
(1)在等腰三角形ABC中,∠A= 80°,求∠B的度数;
(2)等腰三角形ABC的周长为8,AB= 3,求BC的长.
3. 感受方程思想.
如图1-25,在△ABC中,点D在边AC上,点E在边AB上,且AB= AC,BC= BD,AD= DE= EB,求∠A的度数.

1. 感受化归思想.
如图1-24,等边三角形ABC的边长为1,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC的外部,则阴影部分的周长为
3
.
2. 感受分类思想.
(1)在等腰三角形ABC中,∠A= 80°,求∠B的度数;
50°或20°或80°
(2)等腰三角形ABC的周长为8,AB= 3,求BC的长.
2或2.5
3. 感受方程思想.
如图1-25,在△ABC中,点D在边AC上,点E在边AB上,且AB= AC,BC= BD,AD= DE= EB,求∠A的度数.
45°

答案:1. $3$
2.(1)$50^{\circ}$或$20^{\circ}$或$80^{\circ}$;(2)$2$或$2.5$
3. $45^{\circ}$
2.(1)$50^{\circ}$或$20^{\circ}$或$80^{\circ}$;(2)$2$或$2.5$
3. $45^{\circ}$
解析:
1. 将$\triangle ADE$沿直线$DE$折叠,点$A$落在点$A'$处,所以$AD = A'D$,$AE = A'E$。
则$C_{阴影}=A'D + BD + A'E + CE + BC$
$= (AD + BD) + (AE + CE) + BC$
$= AB + AC + BC$
因为$\triangle ABC$是等边三角形,边长为$1$,所以$C_{阴影}= 1 + 1 + 1 = 3$。
2.(1)当$\angle A$为顶角时:
$\angle B=\frac{1}{2}(180^{\circ}-\angle A)=\frac{1}{2}(180 - 80)=50^{\circ}$
当$\angle A$为底角,$\angle B$为顶角时:
$\angle B=180^{\circ}-2\angle A=180 - 2×80=20^{\circ}$
当$\angle A$为底角,$\angle B$为底角时:
$\angle B = \angle A = 80^{\circ}$
综上,$\angle B$的度数为$50^{\circ}$或$20^{\circ}$或$80^{\circ}$。
(2)若$AB$为腰,$AC$为底:
则$AB = AC = 3$,$BC = 8 - 3 - 3 = 2$
若$AB$为底,$AC$为腰:
则$BC = AC=\frac{8 - 3}{2}=2.5$
综上,$BC$的长为$2$或$2.5$。
3. 设$\angle EBD = x$,因为$DE = EB$,所以$\angle EDB=\angle EBD = x$,$\angle AED = \angle EBD + \angle EDB = 2x$
因为$AD = DE$,所以$\angle A=\angle AED = 2x$
$\angle BDC=\angle A+\angle EBD = 3x$
因为$BC = BD$,所以$\angle C=\angle BDC = 3x$
因为$AB = AC$,所以$\angle ABC=\angle C = 3x$
在$\triangle ABC$中,$\angle A+\angle ABC+\angle C = 180^{\circ}$,即$2x + 3x + 3x=180^{\circ}$
$8x=180^{\circ}$
$x = 22.5^{\circ}$
所以$\angle A=2x = 45^{\circ}$
则$C_{阴影}=A'D + BD + A'E + CE + BC$
$= (AD + BD) + (AE + CE) + BC$
$= AB + AC + BC$
因为$\triangle ABC$是等边三角形,边长为$1$,所以$C_{阴影}= 1 + 1 + 1 = 3$。
2.(1)当$\angle A$为顶角时:
$\angle B=\frac{1}{2}(180^{\circ}-\angle A)=\frac{1}{2}(180 - 80)=50^{\circ}$
当$\angle A$为底角,$\angle B$为顶角时:
$\angle B=180^{\circ}-2\angle A=180 - 2×80=20^{\circ}$
当$\angle A$为底角,$\angle B$为底角时:
$\angle B = \angle A = 80^{\circ}$
综上,$\angle B$的度数为$50^{\circ}$或$20^{\circ}$或$80^{\circ}$。
(2)若$AB$为腰,$AC$为底:
则$AB = AC = 3$,$BC = 8 - 3 - 3 = 2$
若$AB$为底,$AC$为腰:
则$BC = AC=\frac{8 - 3}{2}=2.5$
综上,$BC$的长为$2$或$2.5$。
3. 设$\angle EBD = x$,因为$DE = EB$,所以$\angle EDB=\angle EBD = x$,$\angle AED = \angle EBD + \angle EDB = 2x$
因为$AD = DE$,所以$\angle A=\angle AED = 2x$
$\angle BDC=\angle A+\angle EBD = 3x$
因为$BC = BD$,所以$\angle C=\angle BDC = 3x$
因为$AB = AC$,所以$\angle ABC=\angle C = 3x$
在$\triangle ABC$中,$\angle A+\angle ABC+\angle C = 180^{\circ}$,即$2x + 3x + 3x=180^{\circ}$
$8x=180^{\circ}$
$x = 22.5^{\circ}$
所以$\angle A=2x = 45^{\circ}$
1. 如图,在△ABC和△ABD中,∠C= ∠D= 90°,若利用“AAS”说明△ABC≌△ABD,则需要添加条件
$\angle CAB=\angle DAB$
或$\angle CBA=\angle DBA$
;若利用“HL”说明△ABC≌△ABD,则需要添加条件$AC = AD$
或$BC = BD$
.答案:$\angle CAB=\angle DAB$;$\angle CBA=\angle DBA$;$AC = AD$;$BC = BD$
解析:
若利用“AAS”说明$\triangle ABC\cong \triangle ABD$,已知$\angle C=\angle D = 90^{\circ}$,公共边为$AB$,还需要一对角相等,可添加$\angle CAB=\angle DAB$或$\angle CBA=\angle DBA$。
若利用“HL”说明$\triangle ABC\cong \triangle ABD$,因为$\angle C=\angle D = 90^{\circ}$,$AB$为公共边(斜边),则需要添加一对直角边相等,可添加$AC = AD$或$BC = BD$。
若利用“HL”说明$\triangle ABC\cong \triangle ABD$,因为$\angle C=\angle D = 90^{\circ}$,$AB$为公共边(斜边),则需要添加一对直角边相等,可添加$AC = AD$或$BC = BD$。