活动一:想一想 写一写
完成框图,并利用框图回忆判定三角形全等的方法.
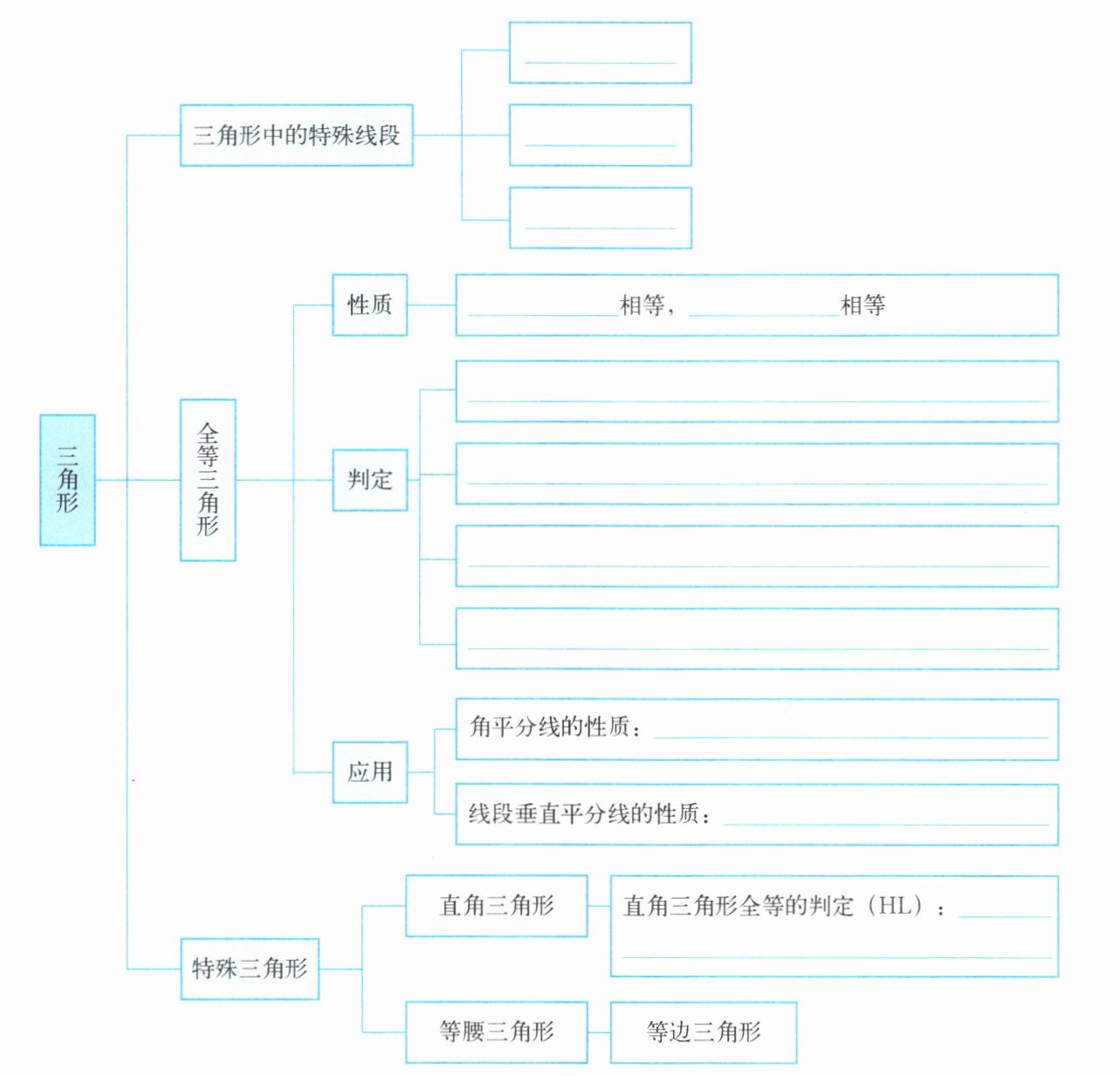
完成框图,并利用框图回忆判定三角形全等的方法.

三角形中的特殊线段:角平分线,中线,高;全等三角形性质:对应边,对应角;判定:SSS,SAS,ASA,AAS;角平分线的性质:角平分线上的点到角的两边的距离相等;线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等;直角三角形全等的判定(HL):斜边和一条直角边对应相等的两个直角三角形全等
答案:三角形中的特殊线段:角平分线,中线,高;全等三角形性质:对应边,对应角;判定:SSS,SAS,ASA,AAS;角平分线的性质:角平分线上的点到角的两边的距离相等;线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等;直角三角形全等的判定(HL):斜边和一条直角边对应相等的两个直角三角形全等
解析:
三角形中的特殊线段包括角平分线、中线、高;全等三角形性质为对应边相等,对应角相等;判定方法有SSS、SAS、ASA、AAS;角平分线性质是角平分线上的点到角两边距离相等;线段垂直平分线性质是线段垂直平分线上的点到线段两端距离相等;直角三角形全等判定(HL)为斜边和一条直角边对应相等的两个直角三角形全等。
活动二:说一说 议一议
与小组成员交流下列问题:
(1)比较线段、角、等腰三角形、等边三角形的性质;
(2)比较线段的垂直平分线和角平分线的性质,比较等腰三角形和等边三角形的性质;
(3)证明线段相等、角相等的常用方法有哪些?
与小组成员交流下列问题:
(1)比较线段、角、等腰三角形、等边三角形的性质;
(2)比较线段的垂直平分线和角平分线的性质,比较等腰三角形和等边三角形的性质;
(3)证明线段相等、角相等的常用方法有哪些?
答案:(1)线段:轴对称图形,垂直平分线上的点到两端距离相等;角:轴对称图形,平分线上的点到两边距离相等;等腰三角形:轴对称图形,两腰等、两底角等(等边对等角),三线合一;等边三角形:轴对称图形(3条对称轴),三边等、三角60°,具等腰三角形所有性质。(2)线段垂直平分线与角平分线:同是轴对称图形,均有点到两端(两边)距离相等性质,前者到端点距离等,后者到两边距离等;等腰与等边三角形:等边三角形是特殊等腰三角形,具其所有性质,等边三角形三边等、三角60°、3条对称轴,等腰三角形两腰等、两底角等、1条对称轴。(3)证明线段相等:全等三角形对应边、等角对等边、线段垂直平分线性质、中点定义、等式性质;证明角相等:全等三角形对应角、等边对等角、平行线性质、对顶角、同(等)角余(补)角、角平分线定义、等式性质。
解析:
(1)线段性质:①轴对称图形(对称轴为垂直平分线);②垂直平分线上的点到两端距离相等。角性质:①轴对称图形(对称轴为角平分线所在直线);②平分线上的点到两边距离相等。等腰三角形性质:①轴对称图形(对称轴为底边上的高所在直线);②两腰相等,两底角相等(等边对等角);③顶角平分线、底边上的中线、底边上的高互相重合(三线合一)。等边三角形性质:①轴对称图形(3条对称轴);②三边相等,三角均为60°;③具有等腰三角形所有性质。
(2)线段垂直平分线与角平分线性质比较:相同点:①轴对称图形;②均有点到两端(或两边)距离相等的性质。不同点:前者到线段两端距离相等,后者到角两边距离相等。等腰三角形与等边三角形性质比较:等边三角形是特殊等腰三角形,具有等腰三角形所有性质;不同点:等边三角形三边相等、三角60°、3条对称轴,等腰三角形两腰相等、两底角相等、1条对称轴。
(3)证明线段相等常用方法:①全等三角形对应边相等;②等角对等边;③线段垂直平分线上的点到两端距离相等;④中点定义;⑤等式性质。证明角相等常用方法:①全等三角形对应角相等;②等边对等角;③平行线的同位角(内错角)相等;④对顶角相等;⑤同角(等角)的余角(补角)相等;⑥角平分线定义;⑦等式性质。
(2)线段垂直平分线与角平分线性质比较:相同点:①轴对称图形;②均有点到两端(或两边)距离相等的性质。不同点:前者到线段两端距离相等,后者到角两边距离相等。等腰三角形与等边三角形性质比较:等边三角形是特殊等腰三角形,具有等腰三角形所有性质;不同点:等边三角形三边相等、三角60°、3条对称轴,等腰三角形两腰相等、两底角相等、1条对称轴。
(3)证明线段相等常用方法:①全等三角形对应边相等;②等角对等边;③线段垂直平分线上的点到两端距离相等;④中点定义;⑤等式性质。证明角相等常用方法:①全等三角形对应角相等;②等边对等角;③平行线的同位角(内错角)相等;④对顶角相等;⑤同角(等角)的余角(补角)相等;⑥角平分线定义;⑦等式性质。