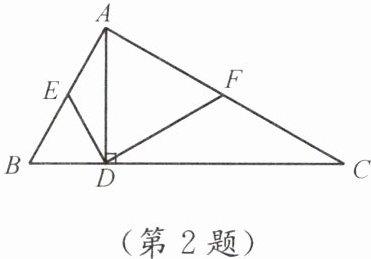
2. 如图,在△ABC中,AD是边BC上的高,DE,DF分别是AB,AC上的中线,AB= 6,AC= 8.求DE+DF的长.

答案:1. 首先,根据直角三角形斜边中线定理:
在$Rt\triangle ABD$中,因为$DE$是斜边$AB$上的中线,根据直角三角形斜边中线定理$DE = \frac{1}{2}AB$(直角三角形斜边中线等于斜边的一半)。
已知$AB = 6$,所以$DE=\frac{1}{2}×6 = 3$。
在$Rt\triangle ACD$中,因为$DF$是斜边$AC$上的中线,根据直角三角形斜边中线定理$DF=\frac{1}{2}AC$(直角三角形斜边中线等于斜边的一半)。
已知$AC = 8$,所以$DF=\frac{1}{2}×8 = 4$。
2. 然后,计算$DE + DF$的值:
$DE+DF=3 + 4$。
所以$DE + DF$的长为$7$。
在$Rt\triangle ABD$中,因为$DE$是斜边$AB$上的中线,根据直角三角形斜边中线定理$DE = \frac{1}{2}AB$(直角三角形斜边中线等于斜边的一半)。
已知$AB = 6$,所以$DE=\frac{1}{2}×6 = 3$。
在$Rt\triangle ACD$中,因为$DF$是斜边$AC$上的中线,根据直角三角形斜边中线定理$DF=\frac{1}{2}AC$(直角三角形斜边中线等于斜边的一半)。
已知$AC = 8$,所以$DF=\frac{1}{2}×8 = 4$。
2. 然后,计算$DE + DF$的值:
$DE+DF=3 + 4$。
所以$DE + DF$的长为$7$。
3. 如图,在△ABC中,点D在AB上,且CD= CB,E为BD的中点,F为AC的中点,连接EF,与CD交于点M,连接AM.
(1)求线段EF,AC之间的数量关系;
(2)若∠BAC= 45°,求线段AM,DM,BC之间的数量关系.

(1)求线段EF,AC之间的数量关系;
(2)若∠BAC= 45°,求线段AM,DM,BC之间的数量关系.

答案:(1) 连接CE。
∵CD=CB,E为BD中点,
∴CE⊥BD(等腰三角形三线合一),即∠CEA=90°。
在Rt△CEA中,F为AC中点,
∴EF=1/2AC(直角三角形斜边上的中线等于斜边的一半)。
(2) ∵∠BAC=45°,F为AC中点,由(1)知EF=1/2AC=AF=FC,
∴AF=EF,△AFE中∠FAE=∠FEA=45°,
∴∠AFE=90°,即EF⊥AC。
∵F为AC中点,EF⊥AC,
∴EF垂直平分AC,又M在EF上,
∴MA=MC(垂直平分线上的点到两端距离相等)。
∵M在CD上,CD=BC,
∴MC=CD-DM=BC-DM,
∴AM=BC-DM,即AM+DM=BC。
(1) EF=1/2AC
(2) AM+DM=BC
∵CD=CB,E为BD中点,
∴CE⊥BD(等腰三角形三线合一),即∠CEA=90°。
在Rt△CEA中,F为AC中点,
∴EF=1/2AC(直角三角形斜边上的中线等于斜边的一半)。
(2) ∵∠BAC=45°,F为AC中点,由(1)知EF=1/2AC=AF=FC,
∴AF=EF,△AFE中∠FAE=∠FEA=45°,
∴∠AFE=90°,即EF⊥AC。
∵F为AC中点,EF⊥AC,
∴EF垂直平分AC,又M在EF上,
∴MA=MC(垂直平分线上的点到两端距离相等)。
∵M在CD上,CD=BC,
∴MC=CD-DM=BC-DM,
∴AM=BC-DM,即AM+DM=BC。
(1) EF=1/2AC
(2) AM+DM=BC
1. 如图,在△ABC中,CF⊥AB,垂足为F,BE⊥AC,垂足为E,M是BC的中点,则图中等腰三角形有 (

A.2个
B.3个
C.4个
D.5个
D
)
A.2个
B.3个
C.4个
D.5个
答案:D
解析:
在△ABC中,CF⊥AB,BE⊥AC,M是BC中点。
1. Rt△BFC中:M为斜边BC中点,由直角三角形斜边中线性质得MF=BM=MC,故△BMF(BM=MF)、△CMF(MC=MF)为等腰三角形。
2. Rt△BEC中:M为斜边BC中点,同理得ME=BM=MC,故△BME(BM=ME)、△CME(MC=ME)为等腰三角形。
3. △FME中:由MF=BM=MC,ME=BM=MC,得MF=ME,故△FME为等腰三角形。
综上,共有5个等腰三角形。
1. Rt△BFC中:M为斜边BC中点,由直角三角形斜边中线性质得MF=BM=MC,故△BMF(BM=MF)、△CMF(MC=MF)为等腰三角形。
2. Rt△BEC中:M为斜边BC中点,同理得ME=BM=MC,故△BME(BM=ME)、△CME(MC=ME)为等腰三角形。
3. △FME中:由MF=BM=MC,ME=BM=MC,得MF=ME,故△FME为等腰三角形。
综上,共有5个等腰三角形。
2. 如图,在四边形ABCD中,∠ABC= ∠ADC= 90°,M,N分别是AC,BD的中点,试说明:
(1)MD= MB;
(2)MN⊥BD.

(1)MD= MB;
(2)MN⊥BD.

答案:(1)
在$\triangle ABC$中,因为$\angle ABC = 90^{\circ}$,$M$是$AC$中点,根据直角三角形斜边中线等于斜边的一半,可得$MB=\frac{1}{2}AC$。
在$\triangle ADC$中,因为$\angle ADC = 90^{\circ}$,$M$是$AC$中点,同理可得$MD=\frac{1}{2}AC$。
所以$MD = MB$。
(2)
由(1)知$MB = MD$,又$N$是$BD$中点,根据等腰三角形三线合一(等腰三角形底边上的中线、底边上的高和顶角平分线互相重合),可得$MN\perp BD$。
在$\triangle ABC$中,因为$\angle ABC = 90^{\circ}$,$M$是$AC$中点,根据直角三角形斜边中线等于斜边的一半,可得$MB=\frac{1}{2}AC$。
在$\triangle ADC$中,因为$\angle ADC = 90^{\circ}$,$M$是$AC$中点,同理可得$MD=\frac{1}{2}AC$。
所以$MD = MB$。
(2)
由(1)知$MB = MD$,又$N$是$BD$中点,根据等腰三角形三线合一(等腰三角形底边上的中线、底边上的高和顶角平分线互相重合),可得$MN\perp BD$。