1. 三角形的角平分线是(
A.直线
B.射线
C.线段
D.射线或线段
C
)A.直线
B.射线
C.线段
D.射线或线段
答案:C
解析:
三角形的角平分线定义是从一个角的顶点出发,将该角平分,并与对边相交,连接这个顶点和交点的线段。根据这个定义,三角形的角平分线是一个线段,而不是直线或射线。
2. 下列图形中,线段BE是△ABC的高的是(
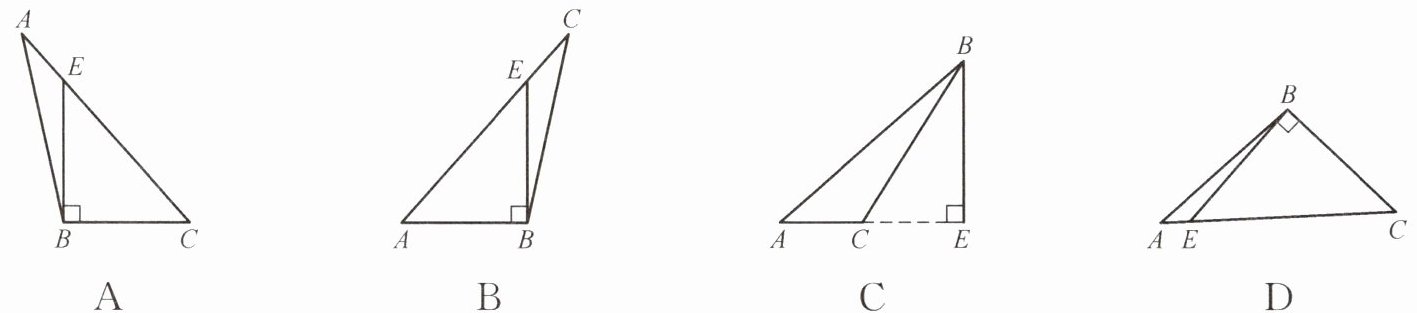
D
)
答案:D
解析:
根据三角形高的定义,从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。选项D中,BE垂直于AC,且垂足E在AC上,所以BE是△ABC的高。
3. 在△ABC中,AD是角平分线,BE是中线.若∠BAD= 40°,则∠CAD=
40°
;若AC= 6,则AE= 3
.答案:$40^\circ$;3
解析:
1. 由于$AD$是角平分线,根据角平分线的性质,有$\angle BAD = \angle CAD$。
已知$\angle BAD = 40^\circ$,所以$\angle CAD = 40^\circ$。
2. 由于$BE$是中线,根据中线的性质,有$AE = \frac{1}{2}AC$。
已知$AC = 6$,所以$AE = 3$。
已知$\angle BAD = 40^\circ$,所以$\angle CAD = 40^\circ$。
2. 由于$BE$是中线,根据中线的性质,有$AE = \frac{1}{2}AC$。
已知$AC = 6$,所以$AE = 3$。
4. 如图,△ABC的高、中线和角平分线都为AD,则∠
BAD
= ∠DAC,BD=DC
= $\frac{1}{2}$BC
.答案:BAD;DC;BC
解析:
因为AD是△ABC的角平分线,所以∠BAD=∠DAC;因为AD是△ABC的中线,所以BD=DC=$\frac{1}{2}$BC。
5. 如图,在△ABC中,D为BC的中点,点E在边AB上(不与点A,B重合),连接DE,△BED的面积与四边形ACDE的面积相等吗?请说明理由.


答案:解:$\triangle BED$的面积与四边形$ACDE$的面积不相等。
理由如下:
因为$D$为$BC$中点,所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$(等底等高的三角形面积相等,$BD = DC$,$\triangle ABD$与$\triangle ACD$高相同)。
又因为$S_{\triangle BED}<S_{\triangle ABD}$($E$在$AB$上且不与$A$、$B$重合),而$S_{四边形ACDE}=S_{\triangle ACD}+S_{\triangle ADE}$,$S_{\triangle ADE}>0$,所以$S_{\triangle BED}\neq S_{四边形ACDE}$。
理由如下:
因为$D$为$BC$中点,所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$(等底等高的三角形面积相等,$BD = DC$,$\triangle ABD$与$\triangle ACD$高相同)。
又因为$S_{\triangle BED}<S_{\triangle ABD}$($E$在$AB$上且不与$A$、$B$重合),而$S_{四边形ACDE}=S_{\triangle ACD}+S_{\triangle ADE}$,$S_{\triangle ADE}>0$,所以$S_{\triangle BED}\neq S_{四边形ACDE}$。
1. 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠BDC= 3∠A,则∠A的度数为

36
°.
答案:36
解析:
设$\angle A = x$。
因为$\angle BDC = 3\angle A$,
所以$\angle BDC = 3x$。
因为$BD$平分$\angle ABC$,$CD$平分$\angle BCA$,
所以设$\angle DBC=\frac{1}{2}\angle ABC$,$\angle DCB=\frac{1}{2}\angle ACB$。
在$\triangle BDC$中,$\angle DBC + \angle DCB + \angle BDC = 180^{\circ}$,
即$\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB + 3x = 180^{\circ}$。
在$\triangle ABC$中,$\angle ABC + \angle ACB + \angle A = 180^{\circ}$,
所以$\angle ABC + \angle ACB = 180^{\circ} - x$。
将$\angle ABC + \angle ACB = 180^{\circ} - x$代入$\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB + 3x = 180^{\circ}$中,
得$\frac{1}{2}(180^{\circ} - x)+3x = 180^{\circ}$。
展开式子得$90^{\circ}-\frac{1}{2}x + 3x = 180^{\circ}$。
移项合并同类项得$\frac{5}{2}x = 90^{\circ}$。
解得$x = 36^{\circ}$,即$\angle A = 36^{\circ}$。
因为$\angle BDC = 3\angle A$,
所以$\angle BDC = 3x$。
因为$BD$平分$\angle ABC$,$CD$平分$\angle BCA$,
所以设$\angle DBC=\frac{1}{2}\angle ABC$,$\angle DCB=\frac{1}{2}\angle ACB$。
在$\triangle BDC$中,$\angle DBC + \angle DCB + \angle BDC = 180^{\circ}$,
即$\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB + 3x = 180^{\circ}$。
在$\triangle ABC$中,$\angle ABC + \angle ACB + \angle A = 180^{\circ}$,
所以$\angle ABC + \angle ACB = 180^{\circ} - x$。
将$\angle ABC + \angle ACB = 180^{\circ} - x$代入$\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB + 3x = 180^{\circ}$中,
得$\frac{1}{2}(180^{\circ} - x)+3x = 180^{\circ}$。
展开式子得$90^{\circ}-\frac{1}{2}x + 3x = 180^{\circ}$。
移项合并同类项得$\frac{5}{2}x = 90^{\circ}$。
解得$x = 36^{\circ}$,即$\angle A = 36^{\circ}$。