3. 设m是$\sqrt{5}$的整数部分,n是$\sqrt{5}$的小数部分,求$m-n$的值.
答案:答题卡:
3.
首先,确定$\sqrt{5}$的范围。
由于$2^2 = 4 \lt 5$ 且 $3^2 = 9 \gt 5$,
所以$2 \lt \sqrt{5} \lt 3$。
根据这个范围,可以确定$\sqrt{5}$的整数部分$m$和小数部分$n$。
整数部分$m = 2$,
小数部分$n = \sqrt{5} - 2$。
最后,计算$m - n$的值。
$m - n = 2 - (\sqrt{5} - 2) = 4 - \sqrt{5}$。
综上,$m-n$的值为$4 - \sqrt{5}$。
3.
首先,确定$\sqrt{5}$的范围。
由于$2^2 = 4 \lt 5$ 且 $3^2 = 9 \gt 5$,
所以$2 \lt \sqrt{5} \lt 3$。
根据这个范围,可以确定$\sqrt{5}$的整数部分$m$和小数部分$n$。
整数部分$m = 2$,
小数部分$n = \sqrt{5} - 2$。
最后,计算$m - n$的值。
$m - n = 2 - (\sqrt{5} - 2) = 4 - \sqrt{5}$。
综上,$m-n$的值为$4 - \sqrt{5}$。
4. 我们可以用"无限逼近法"或借助计算器估算无理数的近似值,我们还可以用以下方法估算无理数的近似值:
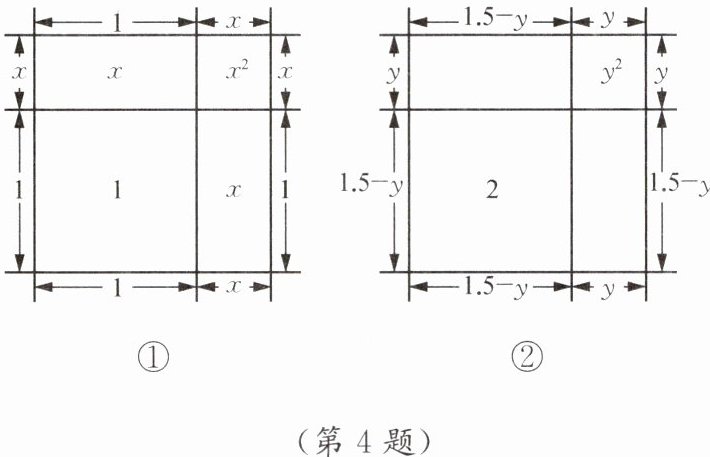
面积为2的正方形的边长为$\sqrt{2}$,且$\sqrt{2}>1$.因此可设$\sqrt{2}= 1+x$,并画出如图①所示的示意图.
根据图①中的面积关系,得$x^{2}+2x+1= 2$.忽略$x^{2}$,得$2x+1\approx2$.解得$x\approx0.5$.所以$\sqrt{2}= 1+x\approx1.5$.因为$\sqrt{2}<1.5$.所以可设$\sqrt{2}= 1.5-y$,并画出如图②所示的示意图……
把上述内容结合如图②所示的示意图,计算出$\sqrt{2}$更加准确的近似值.(结果精确到0.001)
面积为2的正方形的边长为$\sqrt{2}$,且$\sqrt{2}>1$.因此可设$\sqrt{2}= 1+x$,并画出如图①所示的示意图.
根据图①中的面积关系,得$x^{2}+2x+1= 2$.忽略$x^{2}$,得$2x+1\approx2$.解得$x\approx0.5$.所以$\sqrt{2}= 1+x\approx1.5$.因为$\sqrt{2}<1.5$.所以可设$\sqrt{2}= 1.5-y$,并画出如图②所示的示意图……
把上述内容结合如图②所示的示意图,计算出$\sqrt{2}$更加准确的近似值.(结果精确到0.001)

答案:设$\sqrt{2}=1.5 - y$,则$(1.5 - y)^2 = 2$。
展开得:$1.5^2 - 2×1.5× y + y^2 = 2$,即$2.25 - 3y + y^2 = 2$。
忽略$y^2$($y$较小,$y^2$更小),得$2.25 - 3y \approx 2$。
解得:$3y \approx 2.25 - 2 = 0.25$,$y \approx 0.25÷3 \approx 0.0833$。
则$\sqrt{2}=1.5 - y \approx 1.5 - 0.0833 = 1.4167$,精确到$0.001$为$1.417$。
1.417
展开得:$1.5^2 - 2×1.5× y + y^2 = 2$,即$2.25 - 3y + y^2 = 2$。
忽略$y^2$($y$较小,$y^2$更小),得$2.25 - 3y \approx 2$。
解得:$3y \approx 2.25 - 2 = 0.25$,$y \approx 0.25÷3 \approx 0.0833$。
则$\sqrt{2}=1.5 - y \approx 1.5 - 0.0833 = 1.4167$,精确到$0.001$为$1.417$。
1.417