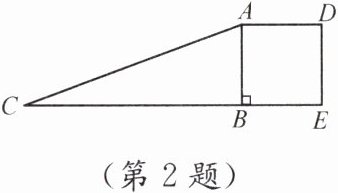
2. 如图,在Rt△ABC中,∠ABC= 90°,AC= 16,BC= 12.求以AB为边的正方形ABED的边长.

答案:在$Rt\triangle ABC$中,$\angle ABC=90^{\circ}$,$AC=16$,$BC=12$。
根据勾股定理$AB^{2}+BC^{2}=AC^{2}$,可得$AB=\sqrt{AC^{2}-BC^{2}}$。
把$AC = 16$,$BC = 12$代入得:
$AB=\sqrt{16^{2}-12^{2}}=\sqrt{(16 + 12)×(16 - 12)}=\sqrt{28×4}=\sqrt{112}=4\sqrt{7}$。
因为正方形$ABED$的边长为$AB$,所以正方形$ABED$的边长为$4\sqrt{7}$。
根据勾股定理$AB^{2}+BC^{2}=AC^{2}$,可得$AB=\sqrt{AC^{2}-BC^{2}}$。
把$AC = 16$,$BC = 12$代入得:
$AB=\sqrt{16^{2}-12^{2}}=\sqrt{(16 + 12)×(16 - 12)}=\sqrt{28×4}=\sqrt{112}=4\sqrt{7}$。
因为正方形$ABED$的边长为$AB$,所以正方形$ABED$的边长为$4\sqrt{7}$。
3. 如图,长2.5 m的梯子靠在墙上,梯子的底端到墙底端的距离为1.5 m.求梯子顶端到地面的距离h.


答案:∵梯子、地面和墙构成直角三角形,梯子为斜边,已知梯子长$2.5m$,底端离墙底端$1.5m$。
根据勾股定理$a^2 + b^2 = c^2$(其中$c$为斜边,$a$、$b$为两直角边),设梯子顶端到地面的距离为$h$,则$h^2+1.5^2 = 2.5^2$。
$h^2=2.5^2 - 1.5^2$
$h^2=(2.5 + 1.5)(2.5 - 1.5)$
$h^2=4×1$
$h^2 = 4$
$h=\pm2$
∵距离不能为负
∴$h = 2$
∴梯子顶端到地面的距离$h$为$2m$。
根据勾股定理$a^2 + b^2 = c^2$(其中$c$为斜边,$a$、$b$为两直角边),设梯子顶端到地面的距离为$h$,则$h^2+1.5^2 = 2.5^2$。
$h^2=2.5^2 - 1.5^2$
$h^2=(2.5 + 1.5)(2.5 - 1.5)$
$h^2=4×1$
$h^2 = 4$
$h=\pm2$
∵距离不能为负
∴$h = 2$
∴梯子顶端到地面的距离$h$为$2m$。
4. 在△ABC中,∠C= 90°,a:b= 3:4,c= 10.求a,b.
答案:答题卡:
解:
设$a = 3x$,$b = 4x$。
根据勾股定理,在直角三角形ABC中,有$a^{2} + b^{2} = c^{2}$。
代入$a = 3x$,$b = 4x$,$c = 10$,得到方程:
$(3x)^{2} + (4x)^{2} = 10^{2}$
$9x^{2} + 16x^{2} = 100$
$25x^{2} = 100$
$x^{2} = 4$
解得$x = 2$或$x = -2$(边长不能为负,舍去)。
所以,$a = 3x = 3 × 2 = 6$,$b = 4x = 4 × 2 = 8$。
答:$a = 6$,$b = 8$。
解:
设$a = 3x$,$b = 4x$。
根据勾股定理,在直角三角形ABC中,有$a^{2} + b^{2} = c^{2}$。
代入$a = 3x$,$b = 4x$,$c = 10$,得到方程:
$(3x)^{2} + (4x)^{2} = 10^{2}$
$9x^{2} + 16x^{2} = 100$
$25x^{2} = 100$
$x^{2} = 4$
解得$x = 2$或$x = -2$(边长不能为负,舍去)。
所以,$a = 3x = 3 × 2 = 6$,$b = 4x = 4 × 2 = 8$。
答:$a = 6$,$b = 8$。
解析:
设$a = 3k$,$b = 4k$($k>0$)。
因为在$\triangle ABC$中,$\angle C = 90^\circ$,根据勾股定理可得$a^2 + b^2 = c^2$。
已知$c = 10$,则$(3k)^2 + (4k)^2 = 10^2$,即$9k^2 + 16k^2 = 100$,$25k^2 = 100$,$k^2 = 4$,解得$k = 2$($k=-2$舍去)。
所以$a = 3k = 3×2 = 6$,$b = 4k = 4×2 = 8$。
$a = 6$,$b = 8$。
因为在$\triangle ABC$中,$\angle C = 90^\circ$,根据勾股定理可得$a^2 + b^2 = c^2$。
已知$c = 10$,则$(3k)^2 + (4k)^2 = 10^2$,即$9k^2 + 16k^2 = 100$,$25k^2 = 100$,$k^2 = 4$,解得$k = 2$($k=-2$舍去)。
所以$a = 3k = 3×2 = 6$,$b = 4k = 4×2 = 8$。
$a = 6$,$b = 8$。
5. 在数轴上画出√13对应的点.


答案:1. 因为$3^2 + 2^2=9 + 4 = 13$,所以在数轴上,以原点$O$为直角顶点,在数轴正半轴上取$OA = 3$,过点$A$作数轴的垂线,在垂线上取$AB=2$。
2. 连接$OB$,根据勾股定理,$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
3. 以$O$为圆心,$OB$为半径画弧,交数轴正半轴于点$C$,则点$C$表示的数就是$\sqrt{13}$。
综上,按照上述步骤可在数轴上画出$\sqrt{13}$对应的点。
2. 连接$OB$,根据勾股定理,$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
3. 以$O$为圆心,$OB$为半径画弧,交数轴正半轴于点$C$,则点$C$表示的数就是$\sqrt{13}$。
综上,按照上述步骤可在数轴上画出$\sqrt{13}$对应的点。
1. 如图,在△ABC中,∠ACB= 90°,AC= 16,BC= 12,CD⊥AB,垂足为D.求AB,CD的长.


答案:在$Rt\triangle ABC$中,根据勾股定理$AB^2 = AC^2 + BC^2$,已知$AC = 16$,$BC = 12$,则$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{16^{2}+12^{2}}=\sqrt{256 + 144}=\sqrt{400}=20$。
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,即$AC\cdot BC = AB\cdot CD$,把$AC = 16$,$BC = 12$,$AB = 20$代入可得$16×12 = 20× CD$,解得$CD=\frac{16×12}{20}=9.6$。
综上,$AB$的长为$20$,$CD$的长为$9.6$。
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,即$AC\cdot BC = AB\cdot CD$,把$AC = 16$,$BC = 12$,$AB = 20$代入可得$16×12 = 20× CD$,解得$CD=\frac{16×12}{20}=9.6$。
综上,$AB$的长为$20$,$CD$的长为$9.6$。
2. 如图,在△ABC中,AB= 15,BC= 14,AC= 13,求△ABC的面积.


答案:过点$A$作$AD\perp BC$于点$D$。
设$BD = x$,则$CD = 14 - x$。
在$Rt\triangle ABD$中,根据勾股定理$AD^{2}=AB^{2}-BD^{2}=15^{2}-x^{2}$。
在$Rt\triangle ACD$中,根据勾股定理$AD^{2}=AC^{2}-CD^{2}=13^{2}-(14 - x)^{2}$。
所以$15^{2}-x^{2}=13^{2}-(14 - x)^{2}$。
展开式子得$225 - x^{2}=169-(196 - 28x+x^{2})$。
去括号得$225 - x^{2}=169 - 196 + 28x - x^{2}$。
移项合并同类项得$28x = 225+(196 - 169)$。
即$28x = 252$,解得$x = 9$。
把$x = 9$代入$AD^{2}=15^{2}-x^{2}$,得$AD^{2}=15^{2}-9^{2}=225 - 81 = 144$,所以$AD = 12$。
根据三角形面积公式$S=\frac{1}{2}× BC× AD$,$BC = 14$,$AD = 12$,则$S_{\triangle ABC}=\frac{1}{2}×14×12 = 84$。
综上,$\triangle ABC$的面积是$84$。
设$BD = x$,则$CD = 14 - x$。
在$Rt\triangle ABD$中,根据勾股定理$AD^{2}=AB^{2}-BD^{2}=15^{2}-x^{2}$。
在$Rt\triangle ACD$中,根据勾股定理$AD^{2}=AC^{2}-CD^{2}=13^{2}-(14 - x)^{2}$。
所以$15^{2}-x^{2}=13^{2}-(14 - x)^{2}$。
展开式子得$225 - x^{2}=169-(196 - 28x+x^{2})$。
去括号得$225 - x^{2}=169 - 196 + 28x - x^{2}$。
移项合并同类项得$28x = 225+(196 - 169)$。
即$28x = 252$,解得$x = 9$。
把$x = 9$代入$AD^{2}=15^{2}-x^{2}$,得$AD^{2}=15^{2}-9^{2}=225 - 81 = 144$,所以$AD = 12$。
根据三角形面积公式$S=\frac{1}{2}× BC× AD$,$BC = 14$,$AD = 12$,则$S_{\triangle ABC}=\frac{1}{2}×14×12 = 84$。
综上,$\triangle ABC$的面积是$84$。