活动一:忆一忆 写一写
写出勾股定理的内容.______
写出勾股定理的内容.______
答案:直角三角形中,两直角边的平方和等于斜边的平方。
解析:
勾股定理描述了直角三角形中三边之间的关系。具体地说,它表明在直角三角形中,直角边的平方和等于斜边的平方。
活动二:做一做 想一想
1. 预习课本第 89~90 页的“问题”,回答以下问题:如课本第 89 页的图 3-6,直接求大正方形面积得 $ S_{正方形ABCD}= $
2. 请你用课本第 90 页的图 3-7 证明勾股定理.
3. 请你用课本第 90 页的图 3-8 证明勾股定理.
1. 预习课本第 89~90 页的“问题”,回答以下问题:如课本第 89 页的图 3-6,直接求大正方形面积得 $ S_{正方形ABCD}= $
$a^2 + 2ab + b^2$
;另一种方法求大正方形面积得 $ S_{正方形ABCD}= $$a^2 + b^2$
;所以得到等式$a^2 + b^2 = c^2$
.2. 请你用课本第 90 页的图 3-7 证明勾股定理.
证明过程如上。
3. 请你用课本第 90 页的图 3-8 证明勾股定理.
证明过程如上。
答案:1. $a^2 + 2ab + b^2$;$a^2 + b^2$;$a^2 + b^2 = c^2$
2. 证明过程如上。
3. 证明过程如上。
2. 证明过程如上。
3. 证明过程如上。
解析:
1. 设直角三角形的两条直角边分别为$a$和$b$,斜边为$c$。
第一种方法:大正方形的边长为$a+b$,所以面积$S_{正方形ABCD} = (a+b)^2 = a^2 + 2ab + b^2$。
第二种方法:大正方形由四个直角三角形和一个小的正方形组成,四个直角三角形的面积总和为$2ab$,小的正方形边长为$c$,面积为$c^2$,所以大正方形的面积也可以表示为$a^2 + b^2 + 2ab - 2ab + c^2 = c^2 + 2ab - 2ab = a^2 + b^2$(这里$2ab - 2ab$是为了展示面积构成,实际计算中可直接得$a^2 + b^2$)。但考虑到四个三角形的面积和为$2ab$,故另一种方法求得的面积为$c^2$(加上四个三角形面积后减去多算的$2ab$),即大正方形面积也等于$a^2 + b^2$(通过等面积法得出)。
所以得到等式:$a^2 + b^2 = c^2$。
2. 对于图3-7的证明:
大正方形面积可以表示为$(a+b)^2$,也可以表示为四个直角三角形的面积(每个为$\frac{1}{2}ab$,共$2ab$)加上中间小正方形的面积$c^2$。
因此,$(a+b)^2 = 4 × \frac{1}{2}ab + c^2$。
展开并化简得:$a^2 + 2ab + b^2 = 2ab + c^2$。
两边减去$2ab$,得:$a^2 + b^2 = c^2$。
3. 对于图3-8的证明(赵爽弦图):
整个图形是一个大正方形,边长为$c$,面积为$c^2$。
它由四个全等的直角三角形(直角边分别为$a$和$b$)和一个小正方形组成。
四个直角三角形的总面积为$4 × \frac{1}{2}ab = 2ab$。
小正方形的边长为$b-a$(或$a-b$,取决于$a$和$b$的大小),面积为$(b-a)^2$。
因此,大正方形的面积也可以表示为$2ab + (b-a)^2$。
展开并化简得:$c^2 = 2ab + b^2 - 2ab + a^2 = a^2 + b^2$。
第一种方法:大正方形的边长为$a+b$,所以面积$S_{正方形ABCD} = (a+b)^2 = a^2 + 2ab + b^2$。
第二种方法:大正方形由四个直角三角形和一个小的正方形组成,四个直角三角形的面积总和为$2ab$,小的正方形边长为$c$,面积为$c^2$,所以大正方形的面积也可以表示为$a^2 + b^2 + 2ab - 2ab + c^2 = c^2 + 2ab - 2ab = a^2 + b^2$(这里$2ab - 2ab$是为了展示面积构成,实际计算中可直接得$a^2 + b^2$)。但考虑到四个三角形的面积和为$2ab$,故另一种方法求得的面积为$c^2$(加上四个三角形面积后减去多算的$2ab$),即大正方形面积也等于$a^2 + b^2$(通过等面积法得出)。
所以得到等式:$a^2 + b^2 = c^2$。
2. 对于图3-7的证明:
大正方形面积可以表示为$(a+b)^2$,也可以表示为四个直角三角形的面积(每个为$\frac{1}{2}ab$,共$2ab$)加上中间小正方形的面积$c^2$。
因此,$(a+b)^2 = 4 × \frac{1}{2}ab + c^2$。
展开并化简得:$a^2 + 2ab + b^2 = 2ab + c^2$。
两边减去$2ab$,得:$a^2 + b^2 = c^2$。
3. 对于图3-8的证明(赵爽弦图):
整个图形是一个大正方形,边长为$c$,面积为$c^2$。
它由四个全等的直角三角形(直角边分别为$a$和$b$)和一个小正方形组成。
四个直角三角形的总面积为$4 × \frac{1}{2}ab = 2ab$。
小正方形的边长为$b-a$(或$a-b$,取决于$a$和$b$的大小),面积为$(b-a)^2$。
因此,大正方形的面积也可以表示为$2ab + (b-a)^2$。
展开并化简得:$c^2 = 2ab + b^2 - 2ab + a^2 = a^2 + b^2$。
1. 根据图片求下列直角三角形相应边的长.
(1)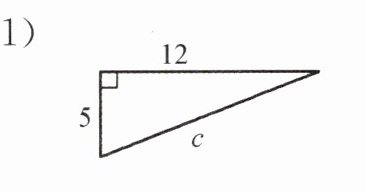
$ c= $
(2)
$ b= $
(1)

$ c= $
13
;(2)

$ b= $
8
.答案:(1) 13
(2) 8
(2) 8
解析:
(1)在直角三角形中,两条直角边的长度分别为5和12,根据勾股定理:
$c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$。
(2)在直角三角形中,一条直角边长为6,斜边长为10,根据勾股定理:
$b = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8$。
$c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$。
(2)在直角三角形中,一条直角边长为6,斜边长为10,根据勾股定理:
$b = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8$。