2. 如图是由一些正方形和直角三角形拼合而成的图形,其中最大正方形的边长为7 cm,则正方形 A,B,C,D 的面积之和为______
49
$.zyjl.cn/pic18/2025-09-04/5b8bd0717a18642b0cea00404644051e.jpg?x-oss-process=image/crop,x_619,y_376,w_278,h_350">$答案:49
解析:
根据勾股定理,直角三角形的两个直角边的平方和等于斜边的平方。
设正方形A, B, C, D的边长分别为a, b, c, d。
图中最大正方形的边长为7 cm,其面积为$7^2 = 49 cm^2$。
观察图形可知,正方形A、B、C、D的边长分别是四个直角三角形的直角边,最大正方形的边长是四个直角三角形的斜边。
根据勾股定理,有:
$ a^2 + b^2 = e^2 $,
$ c^2 + d^2 = f^2 $,
其中e和f分别是两个直角三角形的斜边,且$e^2 + f^2 = 7^2 = 49$。
因此,正方形A, B, C, D的面积之和为:
$ a^2 + b^2 + c^2 + d^2 = e^2 + f^2 = 49 cm^2 $。
设正方形A, B, C, D的边长分别为a, b, c, d。
图中最大正方形的边长为7 cm,其面积为$7^2 = 49 cm^2$。
观察图形可知,正方形A、B、C、D的边长分别是四个直角三角形的直角边,最大正方形的边长是四个直角三角形的斜边。
根据勾股定理,有:
$ a^2 + b^2 = e^2 $,
$ c^2 + d^2 = f^2 $,
其中e和f分别是两个直角三角形的斜边,且$e^2 + f^2 = 7^2 = 49$。
因此,正方形A, B, C, D的面积之和为:
$ a^2 + b^2 + c^2 + d^2 = e^2 + f^2 = 49 cm^2 $。
3. 如图,两个全等的 $ Rt\triangle ADE $,$ Rt\triangle BEC $ 的边 AE,EB 在同一条直线上. 历史上曾有人利用该图形证明了勾股定理,证明中用到的面积相等关系是(
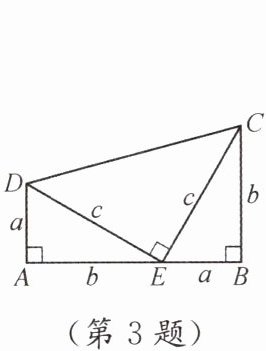
A.$ S_{\triangle EDA}= S_{\triangle CEB} $
B.$ S_{\triangle EDA}+S_{\triangle CEB}= S_{\triangle CDE} $
C.$ S_{四边形C D A E}= S_{四边形C D E B} $
D.$ S_{\triangle EDA}+S_{\triangle CDE}+S_{\triangle CEB}= S_{四边形ABCD} $
D
)
A.$ S_{\triangle EDA}= S_{\triangle CEB} $
B.$ S_{\triangle EDA}+S_{\triangle CEB}= S_{\triangle CDE} $
C.$ S_{四边形C D A E}= S_{四边形C D E B} $
D.$ S_{\triangle EDA}+S_{\triangle CDE}+S_{\triangle CEB}= S_{四边形ABCD} $
答案:D
解析:
由图形可知,四边形ABCD为直角梯形,其面积可表示为$\frac{1}{2}(AD + BC) \cdot AB$。同时,该梯形可分割为$\triangle ADE$、$\triangle CDE$和$\triangle BEC$三个三角形。由于$Rt\triangle ADE \cong Rt\triangle BEC$,设$AD = BE = a$,$AE = BC = b$,$DE = CE = c$,则梯形面积$S_{四边形ABCD} = S_{\triangle EDA} + S_{\triangle CDE} + S_{\triangle CEB}$,此面积关系是证明勾股定理的关键。
1. 如图,小明用 4 个如图①所示的长方形组成图②,其中四边形 ABCD,EFGH,MNPQ 都是正方形. 求证:$ a^{2}+b^{2}= c^{2} $.
 ______
______
 ______
______答案:由题意,图①为长$a$、宽$b$、对角线$c$的长方形,4个图①长方形组成图②,其中ABCD、EFGH、MNPQ为正方形。
1. 大正方形ABCD的面积:
其边长为长方形长与宽之和$a + b$,面积$S_{ABCD}=(a + b)^2=a^2 + 2ab + b^2$。
2. 小正方形MNPQ的面积:
大正方形ABCD面积等于4个长方形面积与MNPQ面积之和。4个长方形面积为$4ab$,设MNPQ边长为$d$,则$a^2 + 2ab + b^2=4ab + d^2$,解得$d^2=(a - b)^2$,即$S_{MNPQ}=(a - b)^2$。
3. 正方形EFGH的面积:
EFGH边长为长方形对角线$c$,面积$S_{EFGH}=c^2$。EFGH面积等于MNPQ面积与4个直角三角形(每个长方形含2个,取其中4个)面积之和,每个直角三角形面积$\frac{1}{2}ab$,4个面积为$2ab$。故$c^2=(a - b)^2 + 2ab$。
4. 化简得结论:
展开$(a - b)^2 + 2ab=a^2 - 2ab + b^2 + 2ab=a^2 + b^2$,即$a^2 + b^2=c^2$。
综上,$a^2 + b^2=c^2$得证。
1. 大正方形ABCD的面积:
其边长为长方形长与宽之和$a + b$,面积$S_{ABCD}=(a + b)^2=a^2 + 2ab + b^2$。
2. 小正方形MNPQ的面积:
大正方形ABCD面积等于4个长方形面积与MNPQ面积之和。4个长方形面积为$4ab$,设MNPQ边长为$d$,则$a^2 + 2ab + b^2=4ab + d^2$,解得$d^2=(a - b)^2$,即$S_{MNPQ}=(a - b)^2$。
3. 正方形EFGH的面积:
EFGH边长为长方形对角线$c$,面积$S_{EFGH}=c^2$。EFGH面积等于MNPQ面积与4个直角三角形(每个长方形含2个,取其中4个)面积之和,每个直角三角形面积$\frac{1}{2}ab$,4个面积为$2ab$。故$c^2=(a - b)^2 + 2ab$。
4. 化简得结论:
展开$(a - b)^2 + 2ab=a^2 - 2ab + b^2 + 2ab=a^2 + b^2$,即$a^2 + b^2=c^2$。
综上,$a^2 + b^2=c^2$得证。
2. 2002 年 8 月,国际数学家大会在北京召开,其会标取材于我国古代数学家赵爽的“弦图”,此图是由 4 个的全等直角三角形和 1 个小正方形构成的大正方形. 如图,若 $ AB= c $,大正方形的面积为 13,中间小正方形的面积为 2,且直角三角形的两直角边分别为 a,b,求 $ (a+b)^{2} $ 的值.
 ______
______
 ______
______答案:24
解析:
由题意知,大正方形面积为13,其边长为直角三角形斜边$c$,则$c^2 = 13$。根据勾股定理,直角三角形两直角边$a,b$满足$a^2 + b^2 = c^2 = 13$。
中间小正方形面积为2,其边长为直角三角形两直角边之差$|a - b|$,则$(a - b)^2 = 2$。展开得$a^2 - 2ab + b^2 = 2$。
将$a^2 + b^2 = 13$代入上式,得$13 - 2ab = 2$,解得$2ab = 11$。
$(a + b)^2 = a^2 + 2ab + b^2 = (a^2 + b^2) + 2ab = 13 + 11 = 24$。
中间小正方形面积为2,其边长为直角三角形两直角边之差$|a - b|$,则$(a - b)^2 = 2$。展开得$a^2 - 2ab + b^2 = 2$。
将$a^2 + b^2 = 13$代入上式,得$13 - 2ab = 2$,解得$2ab = 11$。
$(a + b)^2 = a^2 + 2ab + b^2 = (a^2 + b^2) + 2ab = 13 + 11 = 24$。