活动一:想一想 说一说
预习课本第 97 页,说一说如何设未知数,如何找等量关系列方程.
预习课本第 97 页,说一说如何设未知数,如何找等量关系列方程.
答案:在运用勾股定理解决实际问题时,设未知数通常设题目中所求的未知量为$x$(或其他字母),若所求量较复杂,可设与所求量相关的中间量为未知数。找等量关系的关键是根据题意找出直角三角形,利用勾股定理“直角三角形两直角边的平方和等于斜边的平方”作为等量关系,即若直角边为$a$、$b$,斜边为$c$,则$a^2 + b^2 = c^2$,将已知量和所设未知数代入该等式列方程。
活动二:读一读 议一议
1. 阅读课本第 98 页的例1,想一想:
(1)你能把这个实际问题转化为数学问题吗?说说你的想法.
(2)如何设未知数?如何找等量关系列方程?
(3)说一说勾股定理在问题解决过程中的作用.
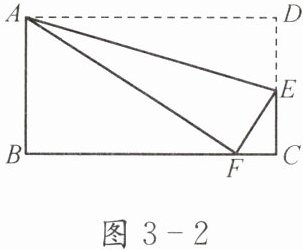
2. 如图 3-2,长方形纸片 ABCD 的边AB= 6 cm,BC= 10 cm,将纸片沿 AE 折叠,使点 D落在边 BC 上的点 F 处.求 DE 的长.
1. 阅读课本第 98 页的例1,想一想:
(1)你能把这个实际问题转化为数学问题吗?说说你的想法.
(2)如何设未知数?如何找等量关系列方程?
(3)说一说勾股定理在问题解决过程中的作用.
2. 如图 3-2,长方形纸片 ABCD 的边AB= 6 cm,BC= 10 cm,将纸片沿 AE 折叠,使点 D落在边 BC 上的点 F 处.求 DE 的长.

答案:1. (1) 能。将实际问题转化为:长方形中,沿一边上的点折叠顶点,求折痕相关线段长度的几何问题,利用折叠性质和勾股定理求解。
(2) 设DE的长为x cm,则EF=x cm,EC=(6-x)cm。由折叠得AF=AD=10cm,在Rt△ABF中用勾股定理求BF,进而得FC,在Rt△EFC中利用勾股定理列方程:FC²+EC²=EF²。
(3) 勾股定理用于在直角三角形中建立边之间的数量关系,通过列方程求解未知线段长度。
2. 设DE=x cm,则EF=x cm,EC=(6-x)cm。
∵折叠,∴AF=AD=10cm。
在Rt△ABF中,AB=6cm,AF=10cm,由勾股定理得:BF=√(AF²-AB²)=√(10²-6²)=8cm。
∴FC=BC-BF=10-8=2cm。
在Rt△EFC中,FC=2cm,EC=(6-x)cm,EF=x cm,由勾股定理得:2²+(6-x)²=x²。
解得:x=10/3。
答:DE的长为10/3 cm。
(2) 设DE的长为x cm,则EF=x cm,EC=(6-x)cm。由折叠得AF=AD=10cm,在Rt△ABF中用勾股定理求BF,进而得FC,在Rt△EFC中利用勾股定理列方程:FC²+EC²=EF²。
(3) 勾股定理用于在直角三角形中建立边之间的数量关系,通过列方程求解未知线段长度。
2. 设DE=x cm,则EF=x cm,EC=(6-x)cm。
∵折叠,∴AF=AD=10cm。
在Rt△ABF中,AB=6cm,AF=10cm,由勾股定理得:BF=√(AF²-AB²)=√(10²-6²)=8cm。
∴FC=BC-BF=10-8=2cm。
在Rt△EFC中,FC=2cm,EC=(6-x)cm,EF=x cm,由勾股定理得:2²+(6-x)²=x²。
解得:x=10/3。
答:DE的长为10/3 cm。
1. 要从电线杆上距离地面5m处向地面拉一条长13m的电缆,则地面电缆固定点与电线杆底部的距离应为 (
A.10 m
B.11 m
C.12 m
D.13 m
C
)A.10 m
B.11 m
C.12 m
D.13 m
答案:C
解析:
设地面电缆固定点与电线杆底部的距离为$x$米,已知电线杆上距离地面5m处拉一条长13m的电缆,根据勾股定理可得$x^{2}+5^{2}=13^{2}$,即$x^{2}=13^{2}-5^{2}=169 - 25 = 144$,解得$x = 12$($x=-12$舍去,因为距离不能为负)。