2. 填空题:
(1)如图①是一个透明的圆柱状的玻璃杯,在其内部测得底面半径为3 cm、高为8 cm,有一支长12 cm的吸管斜放于杯中.若不考虑吸管的粗细,则吸管露出杯口外的长度至少为
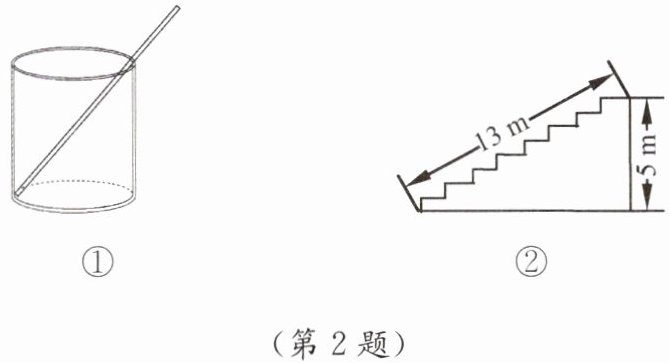
(2)在高5m、长13m的一段台阶上铺地毯,台阶的剖面图如图②,地毯的宽度与台阶的宽度恰好相同,地毯的长度至少为
(1)如图①是一个透明的圆柱状的玻璃杯,在其内部测得底面半径为3 cm、高为8 cm,有一支长12 cm的吸管斜放于杯中.若不考虑吸管的粗细,则吸管露出杯口外的长度至少为
2
cm.
(2)在高5m、长13m的一段台阶上铺地毯,台阶的剖面图如图②,地毯的宽度与台阶的宽度恰好相同,地毯的长度至少为
17
m.答案:(1) 2
(2) 17
(2) 17
解析:
(1) 吸管在圆柱内部最长就是圆柱的对角线长度,根据勾股定理可得:
对角线长度为:$\sqrt{(2×3)^2 + 8^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10$(cm),
吸管总长为12 cm,所以露出杯口外的长度为:$12 - 10 = 2$(cm)。
(2) 台阶的剖面图可以看作一个直角三角形,利用勾股定理,已知斜边为13m,高为5m,
所以水平距离为:$\sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12$(m),
地毯的长度至少为台阶的竖直高度和水平长度之和,即:$5 + 12 = 17$(m)。
对角线长度为:$\sqrt{(2×3)^2 + 8^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10$(cm),
吸管总长为12 cm,所以露出杯口外的长度为:$12 - 10 = 2$(cm)。
(2) 台阶的剖面图可以看作一个直角三角形,利用勾股定理,已知斜边为13m,高为5m,
所以水平距离为:$\sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12$(m),
地毯的长度至少为台阶的竖直高度和水平长度之和,即:$5 + 12 = 17$(m)。
3. 交管部门规定小汽车在某道路上行驶的速度不得超过70 km/h.如图,一辆小汽车在该道路上沿直线行驶,某一时刻刚好行驶到路边车速检测仪A正前方50 m的点C处,4 s后,小汽车与车速检测仪间的距离BA为130 m.这辆小汽车超速了吗?请说明理由.


答案:在$Rt\triangle ABC$中,$AC = 50m$,$AB = 130m$。
由勾股定理可得:
$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{130^{2}-50^{2}}=\sqrt{(130 + 50)(130 - 50)}=\sqrt{180×80}=\sqrt{14400}=120(m)$。
小汽车的速度$v=\frac{120}{4}=30(m/s)$。
因为$1m/s = 3.6km/h$,所以$30m/s=30×3.6 = 108(km/h)$。
由于$108km/h>70km/h$。
综上,这辆小汽车超速了。
由勾股定理可得:
$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{130^{2}-50^{2}}=\sqrt{(130 + 50)(130 - 50)}=\sqrt{180×80}=\sqrt{14400}=120(m)$。
小汽车的速度$v=\frac{120}{4}=30(m/s)$。
因为$1m/s = 3.6km/h$,所以$30m/s=30×3.6 = 108(km/h)$。
由于$108km/h>70km/h$。
综上,这辆小汽车超速了。
1. 如图,在距离地面高4.5 m的墙上装有一盏感应灯A,在距感应灯5 m(含5 m)范围内若有物体,灯就会自动发光.一名身高为1.5 m的学生站在恰好能够使灯发光的位置上,则他距离墙有多远?


答案:设学生距离墙的距离为 $ x $ 米。
学生头顶到感应灯A的垂直距离为 $ 4.5 - 1.5 = 3 $ 米,水平距离为 $ x $ 米,此时学生头顶到A的距离为5米。
由勾股定理得:$ x^2 + 3^2 = 5^2 $
解得:$ x^2 = 25 - 9 = 16 $,$ x = 4 $(负值舍去)
答:他距离墙有4米。
学生头顶到感应灯A的垂直距离为 $ 4.5 - 1.5 = 3 $ 米,水平距离为 $ x $ 米,此时学生头顶到A的距离为5米。
由勾股定理得:$ x^2 + 3^2 = 5^2 $
解得:$ x^2 = 25 - 9 = 16 $,$ x = 4 $(负值舍去)
答:他距离墙有4米。
2. 如图,铁路上A,B两站相距25 km,C,D为两个村庄,DA⊥AB,CB⊥AB,垂足分别为A,B,已知DA= 15 km,CB= 10 km.现要在铁路AB上修建一个土特产收购站E,使得C,D两村到E站的距离相等,E站应修建在离A站多远处?说明理由.


答案:设E站离A站的距离为$ x $km,则E站离B站的距离为$ (25 - x) $km。
在Rt△DAE中,由勾股定理得:$ DE^2 = DA^2 + AE^2 = 15^2 + x^2 $。
在Rt△CBE中,由勾股定理得:$ CE^2 = CB^2 + BE^2 = 10^2 + (25 - x)^2 $。
因为$ DE = CE $,所以$ DE^2 = CE^2 $,即:
$15^2 + x^2 = 10^2 + (25 - x)^2$
展开并化简:
$225 + x^2 = 100 + 625 - 50x + x^2$
$225 = 725 - 50x$
$50x = 500$
$x = 10$
答:E站应修建在离A站10km处。
在Rt△DAE中,由勾股定理得:$ DE^2 = DA^2 + AE^2 = 15^2 + x^2 $。
在Rt△CBE中,由勾股定理得:$ CE^2 = CB^2 + BE^2 = 10^2 + (25 - x)^2 $。
因为$ DE = CE $,所以$ DE^2 = CE^2 $,即:
$15^2 + x^2 = 10^2 + (25 - x)^2$
展开并化简:
$225 + x^2 = 100 + 625 - 50x + x^2$
$225 = 725 - 50x$
$50x = 500$
$x = 10$
答:E站应修建在离A站10km处。