活动三:做一做 想一想
1. 观察平面直角坐标系中各个点的坐标,思考:在各个象限的点的坐标有什么特点?坐标轴上的点的坐标有什么特点?
2. 点P(a,b)到x轴的距离、到y轴的距离、到原点的距离分别如何表示?
1. 观察平面直角坐标系中各个点的坐标,思考:在各个象限的点的坐标有什么特点?坐标轴上的点的坐标有什么特点?
2. 点P(a,b)到x轴的距离、到y轴的距离、到原点的距离分别如何表示?
答案:1. 第一象限$(+,+)$;第二象限$(-,+)$;第三象限$(-,-)$;第四象限$(+,-)$;$x$轴上的点纵坐标为$0$;$y$轴上的点横坐标为$0$。
2. 点$P(a,b)$到$x$轴的距离为$|b|$;到$y$轴的距离为$|a|$;到原点的距离为$\sqrt{a^{2} + b^{2}}$。
2. 点$P(a,b)$到$x$轴的距离为$|b|$;到$y$轴的距离为$|a|$;到原点的距离为$\sqrt{a^{2} + b^{2}}$。
解析:
1. 在平面直角坐标系中,
第一象限的点坐标特点为$(+,+)$,即横坐标和纵坐标都为正;
第二象限的点坐标特点为$(-,+)$,即横坐标为负,纵坐标为正;
第三象限的点坐标特点为$(-,-)$,即横坐标和纵坐标都为负;
第四象限的点坐标特点为$(+,-)$,即横坐标为正,纵坐标为负。
坐标轴上的点,若在$x$轴上,则其纵坐标为$0$;若在$y$轴上,则其横坐标为$0$。
2. 对于点$P(a,b)$,
其到$x$轴的距离为其纵坐标的绝对值,即$|b|$;
其到$y$轴的距离为其横坐标的绝对值,即$|a|$;
利用勾股定理,其到原点的距离为$\sqrt{a^{2} + b^{2}}$。
第一象限的点坐标特点为$(+,+)$,即横坐标和纵坐标都为正;
第二象限的点坐标特点为$(-,+)$,即横坐标为负,纵坐标为正;
第三象限的点坐标特点为$(-,-)$,即横坐标和纵坐标都为负;
第四象限的点坐标特点为$(+,-)$,即横坐标为正,纵坐标为负。
坐标轴上的点,若在$x$轴上,则其纵坐标为$0$;若在$y$轴上,则其横坐标为$0$。
2. 对于点$P(a,b)$,
其到$x$轴的距离为其纵坐标的绝对值,即$|b|$;
其到$y$轴的距离为其横坐标的绝对值,即$|a|$;
利用勾股定理,其到原点的距离为$\sqrt{a^{2} + b^{2}}$。
1. 在平面直角坐标系中,点A(3,-1)位于 (
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:D
解析:
在平面直角坐标系中,第一象限的点坐标符号为(+,+),第二象限的点坐标符号为(-,+),第三象限的点坐标符号为(-,-),第四象限的点坐标符号为(+,-)。
点A的坐标为(3,-1),横坐标为正,纵坐标为负,所以点A位于第四象限。
点A的坐标为(3,-1),横坐标为正,纵坐标为负,所以点A位于第四象限。
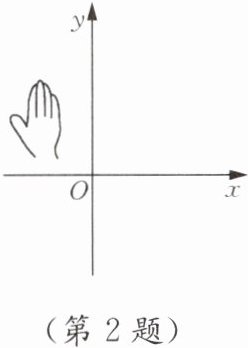
2. 如图,小明用手盖住的点的坐标可能为 (
A.(3,2)
B.(-3,2)
C.(3,-2)
D.(-3,-2)
B
)
A.(3,2)
B.(-3,2)
C.(3,-2)
D.(-3,-2)
答案:B
解析:
由图可知,小明用手盖住的点在第二象限。
在平面直角坐标系中,第二象限的点横坐标为负,纵坐标为正。
选项A中点的坐标$(3,2)$,横坐标$3\gt0$,在第一象限,不符合要求;
选项B中点的坐标$(-3,2)$,横坐标$-3\lt0$,纵坐标$2\gt0$,在第二象限,符合要求;
选项C中点的坐标$(3,-2)$,横坐标$3\gt0$,纵坐标$-2\lt0$,在第四象限,不符合要求;
选项D中点的坐标$(-3,-2)$,横坐标$-3\lt0$,纵坐标$-2\lt0$,在第三象限,不符合要求。
所以小明用手盖住的点的坐标可能为$(-3,2)$。
在平面直角坐标系中,第二象限的点横坐标为负,纵坐标为正。
选项A中点的坐标$(3,2)$,横坐标$3\gt0$,在第一象限,不符合要求;
选项B中点的坐标$(-3,2)$,横坐标$-3\lt0$,纵坐标$2\gt0$,在第二象限,符合要求;
选项C中点的坐标$(3,-2)$,横坐标$3\gt0$,纵坐标$-2\lt0$,在第四象限,不符合要求;
选项D中点的坐标$(-3,-2)$,横坐标$-3\lt0$,纵坐标$-2\lt0$,在第三象限,不符合要求。
所以小明用手盖住的点的坐标可能为$(-3,2)$。
3. 已知点P(m,2)在第一象限,则点B(-3,-m)在第
C
象限.答案:C
解析:
由于点$P(m,2)$在第一象限,根据第一象限的坐标特性(横坐标和纵坐标都为正),可得 $m > 0$。
接下来,考虑点$B(-3, -m)$,由于 $m > 0$,则 $-m < 0$。
点$B$的横坐标为$-3$(负数),纵坐标为$-m$(也是负数)。
根据平面直角坐标系的象限定义,横坐标和纵坐标都为负数的点位于第三象限。
接下来,考虑点$B(-3, -m)$,由于 $m > 0$,则 $-m < 0$。
点$B$的横坐标为$-3$(负数),纵坐标为$-m$(也是负数)。
根据平面直角坐标系的象限定义,横坐标和纵坐标都为负数的点位于第三象限。
4. 在平面直角坐标系中,点P(2,1)到y轴的距离为
2
.答案:2
解析:
在平面直角坐标系中,一个点到$y$轴的距离等于该点横坐标的绝对值。
已知点$P$的坐标为$(2,1)$,其横坐标为$2$,那么点$P$到$y$轴的距离就是$\vert2\vert = 2$。
已知点$P$的坐标为$(2,1)$,其横坐标为$2$,那么点$P$到$y$轴的距离就是$\vert2\vert = 2$。
5. 如图,描出A(-2,1),B(2,-2),C(2,3),D(0,1)四个点,连接AB,BD,DC,CA.求所连线段围成图形的面积.


答案:1. 描点:在坐标系中准确标出A(-2,1)、B(2,-2)、C(2,3)、D(0,1)。
2. 分割图形:连接AD,将四边形ABDC分为△ABD和△ADC。
3. 计算△ADC面积:A(-2,1)、D(0,1)、C(2,3)。AD为水平线段,AD=0-(-2)=2,AD边上的高为C到AD的距离,即3-1=2。面积=1/2×2×2=2。
4. 计算△ABD面积:A(-2,1)、B(2,-2)、D(0,1)。AD为水平线段,AD=2,AD边上的高为B到AD的距离,即1-(-2)=3。面积=1/2×2×3=3。
5. 四边形面积:△ABD面积+△ADC面积=3+2=5。
5
2. 分割图形:连接AD,将四边形ABDC分为△ABD和△ADC。
3. 计算△ADC面积:A(-2,1)、D(0,1)、C(2,3)。AD为水平线段,AD=0-(-2)=2,AD边上的高为C到AD的距离,即3-1=2。面积=1/2×2×2=2。
4. 计算△ABD面积:A(-2,1)、B(2,-2)、D(0,1)。AD为水平线段,AD=2,AD边上的高为B到AD的距离,即1-(-2)=3。面积=1/2×2×3=3。
5. 四边形面积:△ABD面积+△ADC面积=3+2=5。
5