1. 点A(1,-2)向上平移3个单位长度后得到$A_1,$则$A_1$所在的象限为(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:A
解析:
点A(1, -2)向上平移3个单位长度,纵坐标增加3,横坐标不变。
计算得:$A_1$的坐标为$(1, -2 + 3) = (1, 1)$。
横坐标$x = 1 > 0$,纵坐标$y = 1 > 0$,故$A_1$在第一象限。
2. 在平面直角坐标系中,将点A向右平移3个单位长度得到点A'(2,1),点A的坐标是(
A.(5,1)
B.(2,4)
C.(-1,1)
D.(2,-2)
C
)A.(5,1)
B.(2,4)
C.(-1,1)
D.(2,-2)
答案:C
解析:
设点A的坐标为$(x, y)$。
根据平移的性质,当一个点在平面直角坐标系中向右平移$a$个单位长度时,其横坐标增加$a$,纵坐标保持不变。
由题意知,点A向右平移3个单位长度后得到点$A^{\prime}(2,1)$,
因此有:$x + 3 = 2$,$y = 1$,
解这个方程组,得到:$x = -1$,$y = 1$,
所以,点A的坐标是$(-1,1)$。
根据平移的性质,当一个点在平面直角坐标系中向右平移$a$个单位长度时,其横坐标增加$a$,纵坐标保持不变。
由题意知,点A向右平移3个单位长度后得到点$A^{\prime}(2,1)$,
因此有:$x + 3 = 2$,$y = 1$,
解这个方程组,得到:$x = -1$,$y = 1$,
所以,点A的坐标是$(-1,1)$。
3. 在平面直角坐标系中,线段CD是由线段AB平移得到的,已知点A(-1,4)的对应点C的坐标为(3,7),则点B(-4,-1)的对应点D的坐标为______
(0,2)
.答案:D的坐标为(0,2)
解析:
1. 首先,我们需要找出点A到点C的平移向量。点A的坐标为(-1,4),点C的坐标为(3,7)。
2. 计算平移向量:横坐标的变化是 $3 - (-1) = 4$,纵坐标的变化是 $7 - 4 = 3$。
3. 因此,平移向量为 $(4,3)$。
4. 接下来,我们利用这个平移向量来找出点B的对应点D的坐标。点B的坐标为(-4,-1)。
5. 根据平移向量,点D的横坐标为 $-4 + 4 = 0$,纵坐标为 $-1 + 3 = 2$。
6. 所以,点D的坐标为 $(0,2)$。
2. 计算平移向量:横坐标的变化是 $3 - (-1) = 4$,纵坐标的变化是 $7 - 4 = 3$。
3. 因此,平移向量为 $(4,3)$。
4. 接下来,我们利用这个平移向量来找出点B的对应点D的坐标。点B的坐标为(-4,-1)。
5. 根据平移向量,点D的横坐标为 $-4 + 4 = 0$,纵坐标为 $-1 + 3 = 2$。
6. 所以,点D的坐标为 $(0,2)$。
4. 在平面直角坐标系中,将△ABC平移得到$△A_1B_1C_1,$点P(a,b)是△ABC内一点,经平移后得到$△A_1B_1C_1$内对应点$P_1(a+8,b-5),$已知点$A_1$的坐标为(5,-1),则点A的坐标为
(-3,4)
.答案:-3,4
解析:
1. 根据题意,点P(a,b)平移后得到点P₁(a+8,b-5),说明平移向量为右移8个单位,下移5个单位。
2. 平移变换的坐标变化规律为:原坐标(x,y) → (x+8, y-5)。
3. 已知A₁的坐标为(5,-1),设A的坐标为(x,y),则平移后应满足:
x + 8 = 5
y - 5 = -1
4. 解方程组:
x = 5 - 8 = -3
y = -1 + 5 = 4
5. 因此,点A的坐标为(-3,4)。
2. 平移变换的坐标变化规律为:原坐标(x,y) → (x+8, y-5)。
3. 已知A₁的坐标为(5,-1),设A的坐标为(x,y),则平移后应满足:
x + 8 = 5
y - 5 = -1
4. 解方程组:
x = 5 - 8 = -3
y = -1 + 5 = 4
5. 因此,点A的坐标为(-3,4)。
5. △ABC沿x轴正方向平移10个单位长度得到△DEF,△ABC的顶点坐标如图所示.
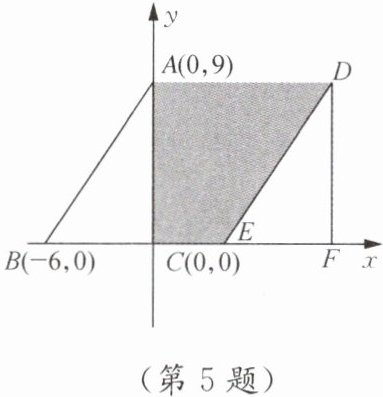
(1) 点D的坐标是
(2) 求四边形ACED的面积.

(1) 点D的坐标是
(10,9)
,点E的坐标是(10,0)
;(2) 求四边形ACED的面积.
解:由平移可知AD//CE,AD=10,CE=10,AC=9。四边形ACED是梯形,根据梯形面积公式可得$S_{四边形ACED}=\frac{(AD + CE)×AC}{2}=\frac{(10 + 10)×9}{2}=90$。所以四边形ACED的面积是90。
答案:1. (1)
因为$\triangle ABC$沿$x$轴正方向平移$10$个单位长度得到$\triangle DEF$,点$A(0,9)$,点$C(0,0)$。
根据平移规律“右加左减,上加下减”(这里是沿$x$轴正方向平移,横坐标加,纵坐标不变),则点$D$的坐标是$(0 + 10,9)$,即$(10,9)$;点$E$的坐标是$(0 + 10,0)$,即$(10,0)$。
2. (2)
解:
由平移可知$AD// CE$,$AD = 10$,$CE = 10$,$AC = 9$。
四边形$ACED$是梯形,根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$是梯形的上底和下底,$h$是梯形的高)。
在四边形$ACED$中,$a = CE=10$,$b = AD = 10$,$h = AC = 9$。
则$S_{四边形ACED}=\frac{(AD + CE)× AC}{2}$。
把$AD = 10$,$CE = 10$,$AC = 9$代入公式得:$S_{四边形ACED}=\frac{(10 + 10)×9}{2}$。
先算括号内$10 + 10=20$,再算$20×9 = 180$,最后算$180÷2=90$。
所以(1)点$D$的坐标是$(10,9)$,点$E$的坐标是$(10,0)$;(2)四边形$ACED$的面积是$90$。
因为$\triangle ABC$沿$x$轴正方向平移$10$个单位长度得到$\triangle DEF$,点$A(0,9)$,点$C(0,0)$。
根据平移规律“右加左减,上加下减”(这里是沿$x$轴正方向平移,横坐标加,纵坐标不变),则点$D$的坐标是$(0 + 10,9)$,即$(10,9)$;点$E$的坐标是$(0 + 10,0)$,即$(10,0)$。
2. (2)
解:
由平移可知$AD// CE$,$AD = 10$,$CE = 10$,$AC = 9$。
四边形$ACED$是梯形,根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$是梯形的上底和下底,$h$是梯形的高)。
在四边形$ACED$中,$a = CE=10$,$b = AD = 10$,$h = AC = 9$。
则$S_{四边形ACED}=\frac{(AD + CE)× AC}{2}$。
把$AD = 10$,$CE = 10$,$AC = 9$代入公式得:$S_{四边形ACED}=\frac{(10 + 10)×9}{2}$。
先算括号内$10 + 10=20$,再算$20×9 = 180$,最后算$180÷2=90$。
所以(1)点$D$的坐标是$(10,9)$,点$E$的坐标是$(10,0)$;(2)四边形$ACED$的面积是$90$。
6. 在平面直角坐标系中,O为原点,点A(0,2),B(-2,0),C(4,0).
(1) 如图①,则△ABC的面积为
(2) 将图①中的点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D,如图②.求△ACD的面积.

(1) 如图①,则△ABC的面积为
6
;(2) 将图①中的点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D,如图②.求△ACD的面积.
18

答案:1. (1)
已知$A(0,2)$,$B(-2,0)$,$C(4,0)$。
根据三角形面积公式$S = \frac{1}{2}×底×高$,在$\triangle ABC$中,以$BC$为底,$BC=\vert - 2-4\vert=6$,$A$点纵坐标的绝对值$\vert y_A\vert$为高,$y_A = 2$。
则$S_{\triangle ABC}=\frac{1}{2}× BC×\vert y_A\vert$,把$BC = 6$,$\vert y_A\vert=2$代入可得$S_{\triangle ABC}=\frac{1}{2}×6×2 = 6$。
2. (2)
解:已知点$B(-2,0)$向右平移$7$个单位长度,再向上平移$4$个单位长度得到点$D$。
根据平移规律“右加左减,上加下减”,则$D$点坐标为$(-2 + 7,0 + 4)$,即$D(5,4)$。
已知$A(0,2)$,$C(4,0)$,$D(5,4)$。
我们用补全图形法求$\triangle ACD$的面积。
过$D$作$DE\perp x$轴于$E$,过$A$作$AF\perp DE$于$F$。
则$S_{\triangle ACD}=S_{梯形AFEC}+S_{\triangle AFD}-S_{\triangle CDE}$。
对于梯形$AFEC$,$AF = 5$,$CE=4$,$EF = 2$,根据梯形面积公式$S_{梯形}=\frac{(上底 + 下底)×高}{2}$,$S_{梯形AFEC}=\frac{(2 + 4)×5}{2}=15$。
对于$\triangle AFD$,$AF = 5$,$FD=4 - 2=2$,根据三角形面积公式$S_{\triangle}=\frac{1}{2}×底×高$,$S_{\triangle AFD}=\frac{1}{2}×5×2 = 5$。
对于$\triangle CDE$,$CE = 1$,$DE = 4$,$S_{\triangle CDE}=\frac{1}{2}×1×4 = 2$。
所以$S_{\triangle ACD}=15 + 5-2=18$。
故答案为:(1)$6$;(2)$18$。
已知$A(0,2)$,$B(-2,0)$,$C(4,0)$。
根据三角形面积公式$S = \frac{1}{2}×底×高$,在$\triangle ABC$中,以$BC$为底,$BC=\vert - 2-4\vert=6$,$A$点纵坐标的绝对值$\vert y_A\vert$为高,$y_A = 2$。
则$S_{\triangle ABC}=\frac{1}{2}× BC×\vert y_A\vert$,把$BC = 6$,$\vert y_A\vert=2$代入可得$S_{\triangle ABC}=\frac{1}{2}×6×2 = 6$。
2. (2)
解:已知点$B(-2,0)$向右平移$7$个单位长度,再向上平移$4$个单位长度得到点$D$。
根据平移规律“右加左减,上加下减”,则$D$点坐标为$(-2 + 7,0 + 4)$,即$D(5,4)$。
已知$A(0,2)$,$C(4,0)$,$D(5,4)$。
我们用补全图形法求$\triangle ACD$的面积。
过$D$作$DE\perp x$轴于$E$,过$A$作$AF\perp DE$于$F$。
则$S_{\triangle ACD}=S_{梯形AFEC}+S_{\triangle AFD}-S_{\triangle CDE}$。
对于梯形$AFEC$,$AF = 5$,$CE=4$,$EF = 2$,根据梯形面积公式$S_{梯形}=\frac{(上底 + 下底)×高}{2}$,$S_{梯形AFEC}=\frac{(2 + 4)×5}{2}=15$。
对于$\triangle AFD$,$AF = 5$,$FD=4 - 2=2$,根据三角形面积公式$S_{\triangle}=\frac{1}{2}×底×高$,$S_{\triangle AFD}=\frac{1}{2}×5×2 = 5$。
对于$\triangle CDE$,$CE = 1$,$DE = 4$,$S_{\triangle CDE}=\frac{1}{2}×1×4 = 2$。
所以$S_{\triangle ACD}=15 + 5-2=18$。
故答案为:(1)$6$;(2)$18$。