1. 把点A(m,m+2)先向左平移2个单位长度,再向上平移3个单位长度得到点B,点B正好落在x轴上,则点B的坐标为(
A.(-5,0)
B.(-7,0)
C.(4,0)
D.(3,0)
B
)A.(-5,0)
B.(-7,0)
C.(4,0)
D.(3,0)
答案:B
解析:
点A(m, m+2)向左平移2个单位后,横坐标变为m-2,纵坐标不变,得到点(m-2, m+2)。再向上平移3个单位,纵坐标变为m+2+3=m+5,得到点B(m-2, m+5)。
由于点B在x轴上,纵坐标为0,即m+5=0,解得m=-5。
代入横坐标m-2,得-5-2=-7,故点B的坐标为(-7, 0)。
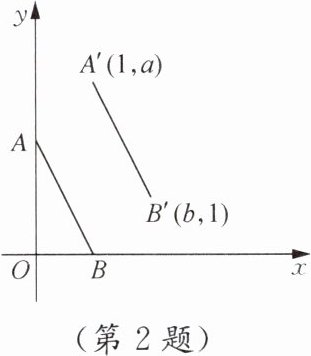
2. 如图,在平面直角坐标系中,点A,B的坐标为(0,2),(1,0),将线段AB平移至A'B'的位置,则a+b的值为(
A.6
B.5
C.4
D.3
B
)
A.6
B.5
C.4
D.3
答案:B
解析:
由题意可知,点$A$的坐标为$(0,2)$,点$B$的坐标为$(1,0)$,将线段$AB$平移至$A'B'$的位置,点$A'$的坐标为$(1,a)$,点$B'$的坐标为$(b,1)$。
平移不改变坐标差值,只改变坐标值,因此:
平移向量在$x$方向上的分量为$1-0=1$,
平移向量在$y$方向上的分量为$a-2$。
同理,点$B$到$B'$的平移向量在$x$方向上的分量为$b-1$,
平移向量在$y$方向上的分量为$1-0=1$。
由于平移向量相同,所以有:
$b-1=1$,$a-2=1$。
解得$b=2$,$a=3$。
所以$a+b=2+3=5$。
平移不改变坐标差值,只改变坐标值,因此:
平移向量在$x$方向上的分量为$1-0=1$,
平移向量在$y$方向上的分量为$a-2$。
同理,点$B$到$B'$的平移向量在$x$方向上的分量为$b-1$,
平移向量在$y$方向上的分量为$1-0=1$。
由于平移向量相同,所以有:
$b-1=1$,$a-2=1$。
解得$b=2$,$a=3$。
所以$a+b=2+3=5$。
3. 对于平面直角坐标系中的图形G和图形G上的任意一点P(x,y),给出如下定义:将点P(x,y)平移到P'(x+t,y-t)称为将点P进行"t型平移",点P'称为将点P进行"t型平移"的对应点;将图形G上的所有点进行"t型平移"称为将图形G进行"t型平移".例如:将点P(x,y)平移到P'(x+1,y-1)称为将点P进行"1型平移",将点P(x,y)平移到P'(x-1,y+1)称为将点P进行"-1型平移".已知点A(1,1)和点B(3,1).
(1) 将点A(1,1)进行"1型平移"后得到的对应点A'的坐标为______;
(2) 将线段AB进行"-1型平移"后得到线段$A_1B_1,P_1(2,3),P_2(1.5,2),P_3(3,0)$三个点中,在线段$A_1B_1$上的点是______;
(3) 若线段AB进行"t型平移"后与坐标轴有公共点,求t的取值范围.

(1)
(2)
(3)
(1) 将点A(1,1)进行"1型平移"后得到的对应点A'的坐标为______;
(2) 将线段AB进行"-1型平移"后得到线段$A_1B_1,P_1(2,3),P_2(1.5,2),P_3(3,0)$三个点中,在线段$A_1B_1$上的点是______;
(3) 若线段AB进行"t型平移"后与坐标轴有公共点,求t的取值范围.

(1)
(2,0)
(2)
P₂
(3)
-3≤t≤-1或t=1
答案:(1)将点$A(1,1)$进行“$1$型平移”,即$t = 1$,根据“$t$型平移”的定义,$x$坐标加$t$,$y$坐标减$t$,可得$A'$的坐标为$(1 + 1,1 - 1)$,即$(2,0)$。
故答案为$(2,0)$。
(2)将线段$AB$进行“$-1$型平移”,即$t = -1$,$A(1,1)$平移后得到$A_1(1 - 1,1 + 1)$,即$A_1(0,2)$;$B(3,1)$平移后得到$B_1(3 - 1,1 + 1)$,即$B_1(2,2)$。
线段$A_1B_1$的方程为$y = 2(0\leq x\leq2)$。
分别将$P_1(2,3)$,$P_2(1.5,2)$,$P_3(3,0)$代入$y = 2$,只有$P_2(1.5,2)$满足。
所以在线段$A_1B_1$上的点是$P_2$。
故答案为$P_2$。
(3)将线段$AB$进行“$t$型平移”后,$A(1,1)$的对应点为$A_2(1 + t,1 - t)$,$B(3,1)$的对应点为$B_2(3 + t,1 - t)$。
当线段$A_2B_2$与$y$轴有公共点时,$1 + t\leq0\leq3 + t$,解不等式$1 + t\leq0$得$t\leq -1$,解不等式$0\leq3 + t$得$t\geq -3$,所以$-3\leq t\leq -1$。
当线段$A_2B_2$与$x$轴有公共点时,$1 - t\leq0\leq1 - t$不成立,考虑端点情况,当$1 - t = 0$时,$t = 1$,此时$A_2(2,0)$,$B_2(4,0)$,满足与$x$轴有公共点;当$3 + t = 0$时,$t = -3$,此时$A_2(-2,4)$,$B_2(0,4)$,也满足与坐标轴有公共点(前面已算过与$y$轴情况),综合可得$t$的取值范围是$-3\leq t\leq -1$或$t = 1$。
故答案为$(2,0)$。
(2)将线段$AB$进行“$-1$型平移”,即$t = -1$,$A(1,1)$平移后得到$A_1(1 - 1,1 + 1)$,即$A_1(0,2)$;$B(3,1)$平移后得到$B_1(3 - 1,1 + 1)$,即$B_1(2,2)$。
线段$A_1B_1$的方程为$y = 2(0\leq x\leq2)$。
分别将$P_1(2,3)$,$P_2(1.5,2)$,$P_3(3,0)$代入$y = 2$,只有$P_2(1.5,2)$满足。
所以在线段$A_1B_1$上的点是$P_2$。
故答案为$P_2$。
(3)将线段$AB$进行“$t$型平移”后,$A(1,1)$的对应点为$A_2(1 + t,1 - t)$,$B(3,1)$的对应点为$B_2(3 + t,1 - t)$。
当线段$A_2B_2$与$y$轴有公共点时,$1 + t\leq0\leq3 + t$,解不等式$1 + t\leq0$得$t\leq -1$,解不等式$0\leq3 + t$得$t\geq -3$,所以$-3\leq t\leq -1$。
当线段$A_2B_2$与$x$轴有公共点时,$1 - t\leq0\leq1 - t$不成立,考虑端点情况,当$1 - t = 0$时,$t = 1$,此时$A_2(2,0)$,$B_2(4,0)$,满足与$x$轴有公共点;当$3 + t = 0$时,$t = -3$,此时$A_2(-2,4)$,$B_2(0,4)$,也满足与坐标轴有公共点(前面已算过与$y$轴情况),综合可得$t$的取值范围是$-3\leq t\leq -1$或$t = 1$。