1. 过点 A(2,-4)和点 B(-4,-4)作直线,则直线 AB (
A.平行于 y 轴
B.平行于 x 轴
C.与 x 轴相交
D.与 x 轴垂直
B
)A.平行于 y 轴
B.平行于 x 轴
C.与 x 轴相交
D.与 x 轴垂直
答案:B
解析:
1. 首先,观察点 A(2,-4)和点 B(-4,-4)的坐标。
2. 注意到两点纵坐标相同,即 $y_A = y_B = -4$。
3. 在平面直角坐标系中,纵坐标相同的点构成的直线平行于 x 轴。
4. 因此,直线 AB 平行于 x 轴。
2. 注意到两点纵坐标相同,即 $y_A = y_B = -4$。
3. 在平面直角坐标系中,纵坐标相同的点构成的直线平行于 x 轴。
4. 因此,直线 AB 平行于 x 轴。
2. 在平面直角坐标系中,已知点 P(1,2),点 Q 在 x 轴下方,且 PQ⊥x 轴. 若 PQ= 5,则点 Q 的坐标为 (
A.(-3,1)
B.(1,-3)
C.(7,1)
D.(1,7)
B
)A.(-3,1)
B.(1,-3)
C.(7,1)
D.(1,7)
答案:B
解析:
1. 已知点 $ P(1,2) $,且点 $ Q $ 在 $ x $ 轴下方,$ PQ $ 垂直于 $ x $ 轴。
2. $ PQ $ 垂直于 $ x $ 轴意味着 $ P $ 和 $ Q $ 的横坐标相同,即 $ Q $ 的横坐标为 1。
3. $ PQ = 5 $,由于 $ Q $ 在 $ x $ 轴下方,$ Q $ 的纵坐标应比 $ P $ 的纵坐标小 5。
4. $ P $ 的纵坐标为 2,因此 $ Q $ 的纵坐标为 $ 2 - 5 = -3 $。
5. 综上,点 $ Q $ 的坐标为 $ (1, -3) $。
2. $ PQ $ 垂直于 $ x $ 轴意味着 $ P $ 和 $ Q $ 的横坐标相同,即 $ Q $ 的横坐标为 1。
3. $ PQ = 5 $,由于 $ Q $ 在 $ x $ 轴下方,$ Q $ 的纵坐标应比 $ P $ 的纵坐标小 5。
4. $ P $ 的纵坐标为 2,因此 $ Q $ 的纵坐标为 $ 2 - 5 = -3 $。
5. 综上,点 $ Q $ 的坐标为 $ (1, -3) $。
3. 下列说法中,正确的有 (
① 若 ab= 0,则点 P(a,b)表示原点
② 点$(1,-a^2)$在第四象限
③ 已知点 A(1,-3)与 B(1,3),则直线 AB 平行于 y 轴
④ 已知点 A(1,-3),AB//y 轴,且 AB= 4,则 B 点的坐标为(1,1)
A.0 个
B.1 个
C.2 个
D.3 个
B
)① 若 ab= 0,则点 P(a,b)表示原点
② 点$(1,-a^2)$在第四象限
③ 已知点 A(1,-3)与 B(1,3),则直线 AB 平行于 y 轴
④ 已知点 A(1,-3),AB//y 轴,且 AB= 4,则 B 点的坐标为(1,1)
A.0 个
B.1 个
C.2 个
D.3 个
答案:B
解析:
① 对于 $ab = 0$,只能说明 $a = 0$ 或 $b = 0$ 或 $a = b = 0$。当 $a = 0$ 且 $b \neq 0$ 时,点 $P(a,b)$ 在 $y$ 轴上;当 $a \neq 0$ 且 $b = 0$ 时,点 $P(a,b)$ 在 $x$ 轴上;当 $a = b = 0$ 时,点 $P(a,b)$ 表示原点。因此,① 错误。
② 对于点 $(1, -a^2)$,由于 $a^2$ 总是非负的,所以 $-a^2 \leq 0$。当 $a = 0$ 时,点在 $x$ 轴上,不在第四象限;当 $a \neq 0$ 时,点在第四象限。因此,不能确定点一定在第四象限,② 错误。
③ 对于点 $A(1, -3)$ 和 $B(1, 3)$,由于它们的横坐标相同,所以直线 $AB$ 平行于 $y$ 轴,③ 正确。
④ 对于点 $A(1, -3)$,且 $AB // y$ 轴,$AB = 4$,则 $B$ 点的横坐标也是 1,纵坐标可以是 $-3 + 4 = 1$ 或 $-3 - 4 = -7$。因此,$B$ 点的坐标可以是 $(1, 1)$ 或 $(1, -7)$,④ 错误(因为它只给出了一个可能的坐标)。
综上所述,只有③是正确的。
② 对于点 $(1, -a^2)$,由于 $a^2$ 总是非负的,所以 $-a^2 \leq 0$。当 $a = 0$ 时,点在 $x$ 轴上,不在第四象限;当 $a \neq 0$ 时,点在第四象限。因此,不能确定点一定在第四象限,② 错误。
③ 对于点 $A(1, -3)$ 和 $B(1, 3)$,由于它们的横坐标相同,所以直线 $AB$ 平行于 $y$ 轴,③ 正确。
④ 对于点 $A(1, -3)$,且 $AB // y$ 轴,$AB = 4$,则 $B$ 点的横坐标也是 1,纵坐标可以是 $-3 + 4 = 1$ 或 $-3 - 4 = -7$。因此,$B$ 点的坐标可以是 $(1, 1)$ 或 $(1, -7)$,④ 错误(因为它只给出了一个可能的坐标)。
综上所述,只有③是正确的。
4. 已知点 A 的坐标为(3,5),且 AB//x 轴,若 AB= 4,则点 B 的坐标为
(7,5)或(-1,5)
.答案:B的坐标为$(7,5)$或$(-1,5)$。
解析:
由于线段$AB$与$x$轴平行,点B的纵坐标应与点A的纵坐标相同,即$y = 5$。
设点B的横坐标为$x$,由于$AB$的长度为4,点A的横坐标为3,根据距离公式,有
$|x - 3| = 4$
解这个方程,得到两个可能的
$x - 3 = 4 \quad 或 \quad x - 3 = -4$
解得$x = 7$或$x = -1$。
因此,点B的可能坐标为$(7, 5)$或$(-1, 5)$。
设点B的横坐标为$x$,由于$AB$的长度为4,点A的横坐标为3,根据距离公式,有
$|x - 3| = 4$
解这个方程,得到两个可能的
$x - 3 = 4 \quad 或 \quad x - 3 = -4$
解得$x = 7$或$x = -1$。
因此,点B的可能坐标为$(7, 5)$或$(-1, 5)$。
5. 在平面直角坐标系中,若第一象限的点 P(x,y)满足 2x+3y= 15,且 x,y 均为整数,则满足条件的点有
2
个.答案:2
解析:
由于点$P(x,y)$在第一象限,所以$x>0$且$y>0$,且$x,y$均为整数。
已知$2x+3y=15$,可以将其改写为$y=\frac{15-2x}{3}=5-\frac{2x}{3}$。
由于$x,y$都是正整数,所以我们需要找出满足这个条件的$x$的值。
首先,$x$必须是$3$的倍数,以保证$y$是整数。
其次,$x$和$y$都必须大于$0$。
当$x=3$时,$y=5-\frac{2×3}{3}=3$,满足条件;
当$x=6$时,$y=5-\frac{2×6}{3}=1$,满足条件;
当$x\geq9$时,$y$将小于$0$,不满足条件。
因此,满足条件的点有$2$个,分别是$(3,3)$和$(6,1)$。
已知$2x+3y=15$,可以将其改写为$y=\frac{15-2x}{3}=5-\frac{2x}{3}$。
由于$x,y$都是正整数,所以我们需要找出满足这个条件的$x$的值。
首先,$x$必须是$3$的倍数,以保证$y$是整数。
其次,$x$和$y$都必须大于$0$。
当$x=3$时,$y=5-\frac{2×3}{3}=3$,满足条件;
当$x=6$时,$y=5-\frac{2×6}{3}=1$,满足条件;
当$x\geq9$时,$y$将小于$0$,不满足条件。
因此,满足条件的点有$2$个,分别是$(3,3)$和$(6,1)$。
6. 如图,在平面直角坐标系中,已知点 A(-3,1),B(-3,-5),点 C(x,y)在线段 AB 上运动,当 OC>OA 时,y 的取值范围为
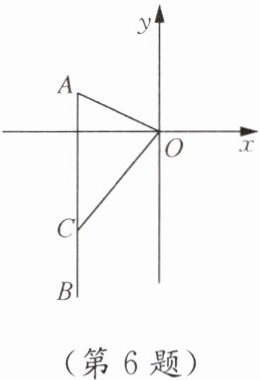
-5 ≤ y < -1
.
答案:-5 ≤ y < -1
解析:
1. 已知点 A(-3,1) 和 B(-3,-5),点 C(x,y) 在线段 AB 上运动。线段 AB 的 x 坐标恒为 -3,y 坐标在 -5 到 1 之间变化。
2. 点 O 为原点 (0,0),OA 的距离为 $\sqrt{(-3)^2 + 1^2} = \sqrt{10}$。
3. 当 OC > OA 时,点 C 的距离 OC 应大于 $\sqrt{10}$。
4. 点 C 的坐标为 (-3, y),OC 的距离为 $\sqrt{(-3)^2 + y^2} = \sqrt{9 + y^2}$。
5. 要使 OC > OA,即 $\sqrt{9 + y^2} > \sqrt{10}$,两边平方得 $9 + y^2 > 10$,即 $y^2 > 1$。
6. 解得 y > 1 或 y < -1。
7. 由于点 C 在线段 AB 上,y 的取值范围在 -5 到 1 之间,因此 y 的实际取值范围为 -5 ≤ y < -1。
2. 点 O 为原点 (0,0),OA 的距离为 $\sqrt{(-3)^2 + 1^2} = \sqrt{10}$。
3. 当 OC > OA 时,点 C 的距离 OC 应大于 $\sqrt{10}$。
4. 点 C 的坐标为 (-3, y),OC 的距离为 $\sqrt{(-3)^2 + y^2} = \sqrt{9 + y^2}$。
5. 要使 OC > OA,即 $\sqrt{9 + y^2} > \sqrt{10}$,两边平方得 $9 + y^2 > 10$,即 $y^2 > 1$。
6. 解得 y > 1 或 y < -1。
7. 由于点 C 在线段 AB 上,y 的取值范围在 -5 到 1 之间,因此 y 的实际取值范围为 -5 ≤ y < -1。
7. 在平面直角坐标系中,已知点 M(m-2,2m-7),点 N(n,3).
(1)若点 M 在 x 轴上,求 m 的值;
(2)若点 M 到 x 轴、y 轴的距离相等,求 m 的值;
(3)若 MN//y 轴,点 M 在点 N 的上方且 MN= 2,求 n 的值.
(1)若点 M 在 x 轴上,求 m 的值;
(2)若点 M 到 x 轴、y 轴的距离相等,求 m 的值;
(3)若 MN//y 轴,点 M 在点 N 的上方且 MN= 2,求 n 的值.
答案:(1) 由于点M在x轴上,其y坐标为0,即:
$2m - 7 = 0$
解得:
$m = \frac{7}{2}$
(2) 点M到x轴的距离为其y坐标的绝对值,即$|2m - 7|$;点M到y轴的距离为其x坐标的绝对值,即$|m - 2|$。
根据题意,这两个距离相等,所以:
$|m - 2| = |2m - 7|$
解此方程得到两个
$m - 2 = 2m - 7 \Rightarrow m = 5$
或
$m - 2 = -(2m - 7) \Rightarrow 3m = 9 \Rightarrow m = 3$
所以,$m = 3$ 或 $m = 5$。
(3) 由于$MN// y$轴,所以M和N的x坐标相同,即:
$m - 2 = n$
又因为点M在点N的上方且$MN = 2$,所以:
$2m - 7 - 3 = 2$
即
$2m - 10 = 2 \Rightarrow 2m = 12 \Rightarrow m = 6$
代入$m - 2 = n$得:
$n = 6 - 2 = 4$
所以,$n = 4$。
$2m - 7 = 0$
解得:
$m = \frac{7}{2}$
(2) 点M到x轴的距离为其y坐标的绝对值,即$|2m - 7|$;点M到y轴的距离为其x坐标的绝对值,即$|m - 2|$。
根据题意,这两个距离相等,所以:
$|m - 2| = |2m - 7|$
解此方程得到两个
$m - 2 = 2m - 7 \Rightarrow m = 5$
或
$m - 2 = -(2m - 7) \Rightarrow 3m = 9 \Rightarrow m = 3$
所以,$m = 3$ 或 $m = 5$。
(3) 由于$MN// y$轴,所以M和N的x坐标相同,即:
$m - 2 = n$
又因为点M在点N的上方且$MN = 2$,所以:
$2m - 7 - 3 = 2$
即
$2m - 10 = 2 \Rightarrow 2m = 12 \Rightarrow m = 6$
代入$m - 2 = n$得:
$n = 6 - 2 = 4$
所以,$n = 4$。
解析:
(1)
∵点M在x轴上,
∴2m-7=0,解得m=$\frac{7}{2}$。
(2)
∵点M到x轴、y轴的距离相等,
∴|m-2|=|2m-7|。
当m-2=2m-7时,解得m=5;
当m-2=-(2m-7)时,解得m=3。
综上,m=3或5。
(3)
∵MN//y轴,
∴n=m-2。
∵点M在点N的上方且MN=2,
∴(2m-7)-3=2,解得m=6。
∴n=6-2=4。