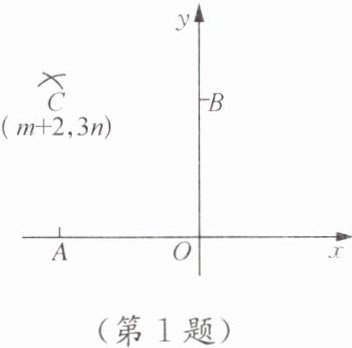
1. 如图,在平面直角坐标系的 x 轴负半轴、y 轴正半轴上分别截取 OA,OB,使 OA= OB,再分别以点 A,B 为圆心,以大于$\frac{1}{2}$AB 长为半径作弧,两弧交于点 C. 若点 C 的坐标为(m+2,3n),则 m 与 n 的关系为 (
A.m-3n= 2
B.3n-m= 3
C.m+3n= -2
D.m+2= 3n
C
)
A.m-3n= 2
B.3n-m= 3
C.m+3n= -2
D.m+2= 3n
答案:C
解析:
分别以点$A,B$为圆心,以大于$\frac{1}{2}AB$长为半径作弧,两弧交于点$C$。
根据垂直平分线的性质:垂直平分线上的点到这条线段两个端点的距离相等,可知点$C$在$AB$的垂直平分线上。
因为$OA = OB$,$\angle AOB = 90^{\circ}$,所以$\triangle AOB$是等腰直角三角形,$AB$的垂直平分线也是第二象限角平分线,其函数解析式为$y = -x$,即第二象限角平分线上的点的横、纵坐标互为相反数。
已知点$C$的坐标为$(m + 2,3n)$,且点$C$在第二象限角平分线上,所以$m + 2 + 3n = 0$,移项可得$m + 3n = -2$。
根据垂直平分线的性质:垂直平分线上的点到这条线段两个端点的距离相等,可知点$C$在$AB$的垂直平分线上。
因为$OA = OB$,$\angle AOB = 90^{\circ}$,所以$\triangle AOB$是等腰直角三角形,$AB$的垂直平分线也是第二象限角平分线,其函数解析式为$y = -x$,即第二象限角平分线上的点的横、纵坐标互为相反数。
已知点$C$的坐标为$(m + 2,3n)$,且点$C$在第二象限角平分线上,所以$m + 2 + 3n = 0$,移项可得$m + 3n = -2$。
2. 在平面直角坐标系中,已知点 A(-2,3),B(2,-1),经过点 A 的直线 l//x 轴,点 C 是直线 l 上的一个动点,当线段 BC 的长度最短时,点 C 的坐标为 (
A.(0,-1)
B.(-1,-2)
C.(-2,-1)
D.(2,3)
D
)A.(0,-1)
B.(-1,-2)
C.(-2,-1)
D.(2,3)
答案:D
3. 在平面直角坐标系中,若一个点的横坐标的 6 倍与纵坐标之差为 6,则称这个点为“如意点”. 下列结论中,错误的是 (
A.(2,6)是“如意点”
B.第二象限内不存在“如意点”
C.若点 P 是“如意点”,且在坐标轴上,则点 P 的坐标为(1,0)
D.已知点 A(-1,-1),B(3,-1),若点 Q 是第四象限内的“如意点”,点 Q 到直线 AB 的距离为 d,则 0≤d<5
C
)A.(2,6)是“如意点”
B.第二象限内不存在“如意点”
C.若点 P 是“如意点”,且在坐标轴上,则点 P 的坐标为(1,0)
D.已知点 A(-1,-1),B(3,-1),若点 Q 是第四象限内的“如意点”,点 Q 到直线 AB 的距离为 d,则 0≤d<5
答案:C
解析:
由“如意点”定义得6x - y = 6,即y = 6x - 6。
A. 当x=2时,y=6×2 - 6=6,(2,6)是“如意点”,A正确;
B. 第二象限x<0,此时y=6x - 6<0,与第二象限y>0矛盾,不存在,B正确;
C. 坐标轴上的点:x轴上y=0,得x=1,即(1,0);y轴上x=0,得y=-6,即(0,-6),故C错误;
D. 直线AB:y=-1,Q在第四象限,x>0,y=6x - 6<0,得0<x<1,距离d=|(6x - 6)-(-1)|=|6x - 5|,0≤d<5,D正确。
A. 当x=2时,y=6×2 - 6=6,(2,6)是“如意点”,A正确;
B. 第二象限x<0,此时y=6x - 6<0,与第二象限y>0矛盾,不存在,B正确;
C. 坐标轴上的点:x轴上y=0,得x=1,即(1,0);y轴上x=0,得y=-6,即(0,-6),故C错误;
D. 直线AB:y=-1,Q在第四象限,x>0,y=6x - 6<0,得0<x<1,距离d=|(6x - 6)-(-1)|=|6x - 5|,0≤d<5,D正确。
4. 如图,在平面直角坐标系中,过点 A(0,4)的直线 a⊥y 轴,M(9,4)为直线 a 上一点. 点 P 从点 M 出发,以每秒 2 个单位长度的速度沿直线 a 向左移动;同时,点 Q 从原点出发,以每秒 1 个单位长度的速度沿 x 轴向右移动. 设运动时间为 t s.
(1)几秒后 AP= OQ?
(2)若以 A,O,Q,P 为顶点的四边形的面积是 10,求点 P 的坐标.

(1)几秒后 AP= OQ?
(2)若以 A,O,Q,P 为顶点的四边形的面积是 10,求点 P 的坐标.

答案:(1) 由题意,点P坐标为(9-2t,4),点Q坐标为(t,0)。
AP=|9-2t|,OQ=t。
AP=OQ得|9-2t|=t。
当t≤4.5时,9-2t=t⇒t=3;
当t>4.5时,2t-9=t⇒t=9。
综上,t=3或t=9。
(2) 四边形AOQP为梯形,高为4,面积S=(AP+OQ)×4÷2=10。
即(|9-2t|+t)×2=10⇒|9-2t|+t=5。
当t≤4.5时,9-2t+t=5⇒t=4,此时P(9-2×4,4)=(1,4);
当t>4.5时,2t-9+t=5⇒t=14/3,此时P(9-2×14/3,4)=(-1/3,4)。
综上,点P坐标为(1,4)或(-1/3,4)。
AP=|9-2t|,OQ=t。
AP=OQ得|9-2t|=t。
当t≤4.5时,9-2t=t⇒t=3;
当t>4.5时,2t-9=t⇒t=9。
综上,t=3或t=9。
(2) 四边形AOQP为梯形,高为4,面积S=(AP+OQ)×4÷2=10。
即(|9-2t|+t)×2=10⇒|9-2t|+t=5。
当t≤4.5时,9-2t+t=5⇒t=4,此时P(9-2×4,4)=(1,4);
当t>4.5时,2t-9+t=5⇒t=14/3,此时P(9-2×14/3,4)=(-1/3,4)。
综上,点P坐标为(1,4)或(-1/3,4)。