活动一:看一看 填一填
1. 四个象限内点的坐标特征:
在图4-4的平面直角坐标系中填上各个象限,并写出对应象限内的点的横、纵坐标的符号.
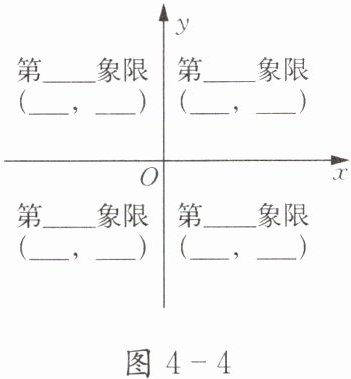

2. 坐标轴上的点的特征:
x轴上的点的______坐标为0,y轴上的点的______坐标为0,原点坐标为______。
3. 与坐标轴平行(或垂直)的直线上的点的特征:
如图4-5,若AB//x轴,则A,B两点的______坐标相同;若CD//y轴,则C,D两点的______坐标相同。
4. 坐标轴所成角的平分线上的点的坐标特征:
(1)两坐标轴正半轴所成角的平分线上的点的特征:______;
(2)两坐标轴负半轴所成角的平分线上的点的特征:______;
(3)x轴负半轴与y轴正半轴所成角的平分线上的点的特征:______;
(4)x轴正半轴与y轴负半轴所成角的平分线上的点的特征:______。
1. 四个象限内点的坐标特征:
在图4-4的平面直角坐标系中填上各个象限,并写出对应象限内的点的横、纵坐标的符号.


一;$(+,+)$;二;$(-,+)$;三;$(-,-)$;四;$(+,-)$
2. 坐标轴上的点的特征:
x轴上的点的______坐标为0,y轴上的点的______坐标为0,原点坐标为______。
纵;横;$(0,0)$
3. 与坐标轴平行(或垂直)的直线上的点的特征:
如图4-5,若AB//x轴,则A,B两点的______坐标相同;若CD//y轴,则C,D两点的______坐标相同。
纵;横
4. 坐标轴所成角的平分线上的点的坐标特征:
(1)两坐标轴正半轴所成角的平分线上的点的特征:______;
横、纵坐标相等
(2)两坐标轴负半轴所成角的平分线上的点的特征:______;
横、纵坐标相等且均为负数
(3)x轴负半轴与y轴正半轴所成角的平分线上的点的特征:______;
横、纵坐标互为相反数且纵坐标为正数
(4)x轴正半轴与y轴负半轴所成角的平分线上的点的特征:______。
横、纵坐标互为相反数且横坐标为正数
答案:1.一;$(+,+)$;二;$(-,+)$;三;$(-,-)$;四;$(+,-)$。
2.纵;横;$(0,0)$。
3.纵;横。
4.(1)横、纵坐标相等;(2)横、纵坐标相等且均为负数;(3)横、纵坐标互为相反数且纵坐标为正数;(4)横、纵坐标互为相反数且横坐标为正数。
2.纵;横;$(0,0)$。
3.纵;横。
4.(1)横、纵坐标相等;(2)横、纵坐标相等且均为负数;(3)横、纵坐标互为相反数且纵坐标为正数;(4)横、纵坐标互为相反数且横坐标为正数。
解析:
1.四个象限内点的坐标特征:
第一象限的点的横坐标为正,纵坐标为正,符号为$(+,+)$。
第二象限的点的横坐标为负,纵坐标为正,符号为$(-,+)$。
第三象限的点的横坐标为负,纵坐标为负,符号为$(-,-)$。
第四象限的点的横坐标为正,纵坐标为负,符号为$(+,-)$。
在图4-4的坐标系中,第一象限填$(+,+)$,第二象限填$(-,+)$,第三象限填$(-,-)$,第四象限填$(+,-)$。
2.坐标轴上的点的特征:
x轴上的点的纵坐标为0,y轴上的点的横坐标为0,原点坐标为$(0,0)$。
3.与坐标轴平行(或垂直)的直线上的点的特征:
若$AB// x$轴,则A,B两点的纵坐标相同。
若$CD// y$轴,则C,D两点的横坐标相同。
4.坐标轴所成角的平分线上的点的坐标特征:
两坐标轴正半轴所成角的平分线上的点的横、纵坐标相等。
两坐标轴负半轴所成角的平分线上的点的横、纵坐标相等且均为负数。
x轴负半轴与y轴正半轴所成角的平分线上的点的横、纵坐标互为相反数且纵坐标为正数。
x轴正半轴与y轴负半轴所成角的平分线上的点的横、纵坐标互为相反数且横坐标为正数。
第一象限的点的横坐标为正,纵坐标为正,符号为$(+,+)$。
第二象限的点的横坐标为负,纵坐标为正,符号为$(-,+)$。
第三象限的点的横坐标为负,纵坐标为负,符号为$(-,-)$。
第四象限的点的横坐标为正,纵坐标为负,符号为$(+,-)$。
在图4-4的坐标系中,第一象限填$(+,+)$,第二象限填$(-,+)$,第三象限填$(-,-)$,第四象限填$(+,-)$。
2.坐标轴上的点的特征:
x轴上的点的纵坐标为0,y轴上的点的横坐标为0,原点坐标为$(0,0)$。
3.与坐标轴平行(或垂直)的直线上的点的特征:
若$AB// x$轴,则A,B两点的纵坐标相同。
若$CD// y$轴,则C,D两点的横坐标相同。
4.坐标轴所成角的平分线上的点的坐标特征:
两坐标轴正半轴所成角的平分线上的点的横、纵坐标相等。
两坐标轴负半轴所成角的平分线上的点的横、纵坐标相等且均为负数。
x轴负半轴与y轴正半轴所成角的平分线上的点的横、纵坐标互为相反数且纵坐标为正数。
x轴正半轴与y轴负半轴所成角的平分线上的点的横、纵坐标互为相反数且横坐标为正数。
活动二:想一想 写一写
1. 在平面直角坐标系中,有一点P(x,y),点P到x轴的距离可以表示为
2. 如图4-5,已知A(xₐ,yₐ),B(xᵦ,yᵦ),AB//x轴,则A,B两点的距离可以表示为
1. 在平面直角坐标系中,有一点P(x,y),点P到x轴的距离可以表示为
|y|
,点P到y轴的距离可以表示为|x|
,点P到原点的距离可以表示为√(x² + y²)
.2. 如图4-5,已知A(xₐ,yₐ),B(xᵦ,yᵦ),AB//x轴,则A,B两点的距离可以表示为
|xₐ - xᵦ|
;已知C(xc,yc),D(xd,yd),CD//y轴,则C,D两点的距离可以表示为|yc - yd|
.答案:1. $|y|$;$|x|$;$\sqrt{x^2 + y^2}$
2. $|x_a - x_b|$;$|y_c - y_d|$
2. $|x_a - x_b|$;$|y_c - y_d|$
解析:
1. 在平面直角坐标系中,一个点$P(x,y)$到$x$轴的距离等于该点的纵坐标的绝对值,即$|y|$;到$y$轴的距离等于该点的横坐标的绝对值,即$|x|$;到原点的距离等于该点到原点的直线距离,根据勾股定理,为$\sqrt{x^2 + y^2}$。
2. 对于点$A(x_a,y_a)$和点$B(x_b,y_b)$,如果线段$AB$平行于$x$轴,那么$A$和$B$的纵坐标相同,即$y_a = y_b$,此时$A$和$B$的距离等于它们横坐标之差的绝对值,即$|x_a - x_b|$;对于点$C(x_c,y_c)$和点$D(x_d,y_d)$,如果线段$CD$平行于$y$轴,那么$C$和$D$的横坐标相同,即$x_c = x_d$,此时$C$和$D$的距离等于它们纵坐标之差的绝对值,即$|y_c - y_d|$。
2. 对于点$A(x_a,y_a)$和点$B(x_b,y_b)$,如果线段$AB$平行于$x$轴,那么$A$和$B$的纵坐标相同,即$y_a = y_b$,此时$A$和$B$的距离等于它们横坐标之差的绝对值,即$|x_a - x_b|$;对于点$C(x_c,y_c)$和点$D(x_d,y_d)$,如果线段$CD$平行于$y$轴,那么$C$和$D$的横坐标相同,即$x_c = x_d$,此时$C$和$D$的距离等于它们纵坐标之差的绝对值,即$|y_c - y_d|$。