活动三:试一试 写一写
在平面直角坐标系中,有一点P(x,y).
(1)将点P沿平行于x轴的方向平移,横坐标
(2)将点P沿平行于y轴的方向平移,横坐标
(3)点P关于x轴对称的点的坐标为
(4)点P关于y轴对称的点的坐标为
(5)点P关于原点对称的点的坐标为
在平面直角坐标系中,有一点P(x,y).
(1)将点P沿平行于x轴的方向平移,横坐标
增加或减少一个值
,纵坐标不变
;(2)将点P沿平行于y轴的方向平移,横坐标
不变
,纵坐标增加或减少一个值
;(3)点P关于x轴对称的点的坐标为
$(x, -y)$
;(4)点P关于y轴对称的点的坐标为
$(-x, y)$
;(5)点P关于原点对称的点的坐标为
$(-x, -y)$
.答案:(1) 增加或减少一个值;不变
(2) 不变;增加或减少一个值
(3) $(x, -y)$
(4) $(-x, y)$
(5) $(-x, -y)$
(2) 不变;增加或减少一个值
(3) $(x, -y)$
(4) $(-x, y)$
(5) $(-x, -y)$
解析:
(1) 当点P沿平行于x轴的方向平移时,其横坐标会发生变化,而纵坐标保持不变。因此,横坐标增加或减少一个值,纵坐标不变。
(2) 当点P沿平行于y轴的方向平移时,其纵坐标会发生变化,而横坐标保持不变。因此,纵坐标增加或减少一个值,横坐标不变。
(3) 点P关于x轴对称的点,其横坐标保持不变,纵坐标变为相反数。
(4) 点P关于y轴对称的点,其纵坐标保持不变,横坐标变为相反数。
(5) 点P关于原点对称的点,其横坐标和纵坐标都变为相反数。
(2) 当点P沿平行于y轴的方向平移时,其纵坐标会发生变化,而横坐标保持不变。因此,纵坐标增加或减少一个值,横坐标不变。
(3) 点P关于x轴对称的点,其横坐标保持不变,纵坐标变为相反数。
(4) 点P关于y轴对称的点,其纵坐标保持不变,横坐标变为相反数。
(5) 点P关于原点对称的点,其横坐标和纵坐标都变为相反数。
1. 若点A(-3,a)在x轴上,则点B(a-1,a+2)在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解析:
1. 点A(-3, a)在x轴上,说明其纵坐标a = 0。
2. 将a = 0代入点B的坐标,得B(a-1, a+2) = B(-1, 2)。
3. 点B的横坐标为-1(负),纵坐标为2(正),因此点B位于第二象限。
2. 将点P先向左平移3个单位长度,再向下平移2个单位长度后得到的对应点Q的坐标为(-4,1),则点P的坐标为(
A.(-1,3)
B.(-4,1)
C.(2,5)
D.(1,0)
A
)A.(-1,3)
B.(-4,1)
C.(2,5)
D.(1,0)
答案:A
解析:
设点P的坐标为(x, y)。
根据平移规律:
向左平移3个单位长度,x坐标减少3,即新的x坐标为$x - 3$;
向下平移2个单位长度,y坐标减少2,即新的y坐标为$y - 2$。
因此,平移后的点Q的坐标为$(x - 3, y - 2)$。
由题意知,点Q的坐标为(-4, 1),
所以我们可以列出方程组:
$\begin{cases}x - 3 = -4 \\y - 2 = 1\end{cases}$
解这个方程组,我们得到:
$\begin{cases}x = -1 \\y = 3\end{cases}$
所以,点P的坐标为(-1, 3)。
根据平移规律:
向左平移3个单位长度,x坐标减少3,即新的x坐标为$x - 3$;
向下平移2个单位长度,y坐标减少2,即新的y坐标为$y - 2$。
因此,平移后的点Q的坐标为$(x - 3, y - 2)$。
由题意知,点Q的坐标为(-4, 1),
所以我们可以列出方程组:
$\begin{cases}x - 3 = -4 \\y - 2 = 1\end{cases}$
解这个方程组,我们得到:
$\begin{cases}x = -1 \\y = 3\end{cases}$
所以,点P的坐标为(-1, 3)。
3. 已知A(2,a),B(b,-3)是平面直角坐标系上的两个点,AB//x轴,且点B在点A的右侧.若AB= 5,则(
A.a= -3,b= -3
B.a= -3,b= 7
C.a= 2,b= 2
D.a= -8,b= 2
B
)A.a= -3,b= -3
B.a= -3,b= 7
C.a= 2,b= 2
D.a= -8,b= 2
答案:B
解析:
由于线段$AB$与$x$轴平行,所以A,B两点的纵坐标相等,即$a = -3$。
设点B的横坐标为$b$,由于点B在点A的右侧,且$AB = 5$,所以有$b - 2 = 5$,解得$b = 7$。
设点B的横坐标为$b$,由于点B在点A的右侧,且$AB = 5$,所以有$b - 2 = 5$,解得$b = 7$。
4. 已知点A(-2,b)与点B(a,3)关于原点对称,则a-b=
5
.答案:5
解析:
已知点$A(-2,b)$与点$B(a,3)$关于原点对称,根据关于原点对称的点的坐标性质,如果两点关于原点对称,则它们的横、纵坐标互为相反数。
因此,有$a = -(-2) = 2$,$b = -(3) = -3$。
进一步计算$a-b$,即$a-b = 2 - (-3) = 2 + 3 = 5$。
因此,有$a = -(-2) = 2$,$b = -(3) = -3$。
进一步计算$a-b$,即$a-b = 2 - (-3) = 2 + 3 = 5$。
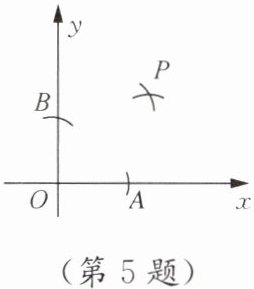
5. 如图,在x轴,y轴上分别截取OA,OB,使OA= OB,再分别以点A,B为圆心,以大于$\frac{1}{2}$AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为______
3
.
答案:3
解析:
由题意知,点P在∠AOB的角平分线上,即点P到x轴和y轴的距离相等。
因为点P的坐标为$(a, 2a - 3)$,所以$|a| = |2a - 3|$。
分两种情况讨论:
1. 当$a = 2a - 3$时,解得$a = 3$;
2. 当$a = -(2a - 3)$时,解得$a = 1$。
由图可知点P在第一象限,所以$a > 0$,$2a - 3 > 0$,即$a > \frac{3}{2}$。因此$a = 1$不符合题意,舍去。
综上,$a$的值为$3$。
3
因为点P的坐标为$(a, 2a - 3)$,所以$|a| = |2a - 3|$。
分两种情况讨论:
1. 当$a = 2a - 3$时,解得$a = 3$;
2. 当$a = -(2a - 3)$时,解得$a = 1$。
由图可知点P在第一象限,所以$a > 0$,$2a - 3 > 0$,即$a > \frac{3}{2}$。因此$a = 1$不符合题意,舍去。
综上,$a$的值为$3$。
3
6. 如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M,N的坐标分别为(3,9),(12,9),则顶点A的坐标为______
(0,3)
$.zyjl.cn/pic18/2025-09-04/a84bfafed547ae74b642a0810a32b119.jpg?x-oss-process=image/crop,x_1019,y_1652,w_295,h_290">$答案:A
解析:
1. 已知顶点M(3,9)和N(12,9),可知MN边水平,长度为$12-3=9$。
2. 五个大小相同的正方形置于直角坐标系中,每个正方形的边长设为$a$。
3. 因为MN边上有三个正方形的边长,所以$3a=9$,解得$a=3$。
4. 从图中可以看出,A点在N点的正下方两个正方形边长的位置,即A点的纵坐标为$9-2a=9-2 × 3=3$。
5. A点的横坐标与N点相同,为12。
6. 因此,顶点A的坐标为(12, 3)。
2. 五个大小相同的正方形置于直角坐标系中,每个正方形的边长设为$a$。
3. 因为MN边上有三个正方形的边长,所以$3a=9$,解得$a=3$。
4. 从图中可以看出,A点在N点的正下方两个正方形边长的位置,即A点的纵坐标为$9-2a=9-2 × 3=3$。
5. A点的横坐标与N点相同,为12。
6. 因此,顶点A的坐标为(12, 3)。
7. 如图,在平面直角坐标系中,已知A(-1,5),B(4,2),C(-1,0).
(1)点A关于原点O的对称点A'的坐标为
(2)连接A'B',B'C',A'C',求△A'B'C'的面积.

(1)点A关于原点O的对称点A'的坐标为
(1, -5)
,点B关于x轴的对称点B'的坐标为(4, -2)
,点C关于y轴的对称点C'的坐标为(1, 0)
.(2)连接A'B',B'C',A'C',求△A'B'C'的面积.

因为$A' (1, -5)$,$B' (4, -2)$,$C' (1, 0)$
所以$A'C'=\vert-5 - 0\vert = 5$,$A'C'$边上的高为$\vert4 - 1\vert = 3$
$S_{\triangle A'B'C'}=\frac{1}{2}× A'C'×3=\frac{1}{2}×5×3 = 7.5$
所以$A'C'=\vert-5 - 0\vert = 5$,$A'C'$边上的高为$\vert4 - 1\vert = 3$
$S_{\triangle A'B'C'}=\frac{1}{2}× A'C'×3=\frac{1}{2}×5×3 = 7.5$
答案:(1) $(1, -5)$;$(4, -2)$;$(1, 0)$
(2) 因为$A' (1, -5)$,$B' (4, -2)$,$C' (1, 0)$
所以$A'C'=\vert-5 - 0\vert = 5$,$A'C'$边上的高为$\vert4 - 1\vert = 3$
$S_{\triangle A'B'C'}=\frac{1}{2}× A'C'×3=\frac{1}{2}×5×3 = 7.5$
(2) 因为$A' (1, -5)$,$B' (4, -2)$,$C' (1, 0)$
所以$A'C'=\vert-5 - 0\vert = 5$,$A'C'$边上的高为$\vert4 - 1\vert = 3$
$S_{\triangle A'B'C'}=\frac{1}{2}× A'C'×3=\frac{1}{2}×5×3 = 7.5$