活动一:想一想 议一议
1. 当两个三角形的一组边或角相等时,它们全等吗?
2. 当两个三角形的两组边或角分别相等时,它们全等吗?
3. 当两个三角形的三组边或角分别相等时,它们全等吗?
1. 当两个三角形的一组边或角相等时,它们全等吗?
2. 当两个三角形的两组边或角分别相等时,它们全等吗?
3. 当两个三角形的三组边或角分别相等时,它们全等吗?
答案:1. 当两个三角形的一组边或角相等时,它们不一定全等。
2. 当两个三角形的两组边或角分别相等时,它们不一定全等。
3. 当两个三角形的三组边分别相等时,根据$SSS$(边边边)全等判定,这两个三角形全等;当两个三角形的三组角分别相等时,它们不一定全等。
2. 当两个三角形的两组边或角分别相等时,它们不一定全等。
3. 当两个三角形的三组边分别相等时,根据$SSS$(边边边)全等判定,这两个三角形全等;当两个三角形的三组角分别相等时,它们不一定全等。
活动二:做一做 比一比
1. (1)利用量角器画∠MAN= 50°;
(2)在 AM,AN 上分别截取 AB= 2 cm,AC= 3 cm;
(3)连接 BC,剪下所画的△ABC,与同学所画的三角形比一比,能够重合吗?
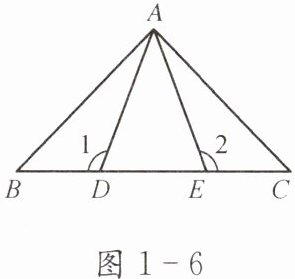
2. 如图 1-6,AD= AE,点 D,E 在 BC 上,BE= CD,∠1= ∠2.
求证:∠B= ∠C.
1. (1)利用量角器画∠MAN= 50°;
(2)在 AM,AN 上分别截取 AB= 2 cm,AC= 3 cm;
(3)连接 BC,剪下所画的△ABC,与同学所画的三角形比一比,能够重合吗?
2. 如图 1-6,AD= AE,点 D,E 在 BC 上,BE= CD,∠1= ∠2.
求证:∠B= ∠C.

答案:1.
(1)按要求利用量角器画出$\angle MAN = 50^{\circ}$;
(2)在$AM$,$AN$上分别截取$AB = 2cm$,$AC = 3cm$;
(3)连接$BC$,剪下所画的$\triangle ABC$,与同学所画的三角形比一比,能够重合。
2.
证明:
因为$BE = CD$,所以$BE - DE = CD - DE$,即$BD = CE$。
又因为$AD = AE$,所以$\angle ADE = \angle AED$,则$\angle ADB = \angle AEC$。
在$\triangle ADB$和$\triangle AEC$中,
$\begin{cases}AD = AE\\\angle ADB = \angle AEC\\BD = CE\end{cases}$
根据$SAS$(边角边)判定定理,可得$\triangle ADB\cong\triangle AEC$。
所以$\angle B = \angle C$。
(1)按要求利用量角器画出$\angle MAN = 50^{\circ}$;
(2)在$AM$,$AN$上分别截取$AB = 2cm$,$AC = 3cm$;
(3)连接$BC$,剪下所画的$\triangle ABC$,与同学所画的三角形比一比,能够重合。
2.
证明:
因为$BE = CD$,所以$BE - DE = CD - DE$,即$BD = CE$。
又因为$AD = AE$,所以$\angle ADE = \angle AED$,则$\angle ADB = \angle AEC$。
在$\triangle ADB$和$\triangle AEC$中,
$\begin{cases}AD = AE\\\angle ADB = \angle AEC\\BD = CE\end{cases}$
根据$SAS$(边角边)判定定理,可得$\triangle ADB\cong\triangle AEC$。
所以$\angle B = \angle C$。