3. 已知△ABC≌△DEF,A 与 D,B 与 E 分别是对应顶点.
(1)若△ABC 的周长为 32,AB= 10,BC= 14,则 AC=
(2)若∠A= 48°,∠B= 53°,则∠D=
(1)若△ABC 的周长为 32,AB= 10,BC= 14,则 AC=
8
,DE= 10
,EF= 14
;(2)若∠A= 48°,∠B= 53°,则∠D=
$48^\circ$
,∠F= $79^\circ$
.答案:(1) 8;10;14
(2) $48^\circ$;$79^\circ$
(2) $48^\circ$;$79^\circ$
解析:
(1)
已知△ABC的周长为32,且$AB = 10$,$BC = 14$。
根据三角形周长的定义,有
$AC = 32 - AB - BC$
$AC = 32 - 10 - 14$
$AC = 8$
由于△ABC≌△DEF,根据全等三角形的性质,对应边相等,即
$DE = AB = 10$
$EF = BC = 14$
(2)
已知∠A = 48°,∠B = 53°。
根据三角形内角和为180°,有
$\angle C = 180^\circ - \angle A - \angle B$
$\angle C = 180^\circ - 48^\circ - 53^\circ$
$\angle C = 79^\circ$
由于△ABC≌△DEF,根据全等三角形的性质,对应角相等,即
$\angle D = \angle A = 48^\circ$
$\angle F = \angle C = 79^\circ$
已知△ABC的周长为32,且$AB = 10$,$BC = 14$。
根据三角形周长的定义,有
$AC = 32 - AB - BC$
$AC = 32 - 10 - 14$
$AC = 8$
由于△ABC≌△DEF,根据全等三角形的性质,对应边相等,即
$DE = AB = 10$
$EF = BC = 14$
(2)
已知∠A = 48°,∠B = 53°。
根据三角形内角和为180°,有
$\angle C = 180^\circ - \angle A - \angle B$
$\angle C = 180^\circ - 48^\circ - 53^\circ$
$\angle C = 79^\circ$
由于△ABC≌△DEF,根据全等三角形的性质,对应角相等,即
$\angle D = \angle A = 48^\circ$
$\angle F = \angle C = 79^\circ$
4. 下列判断中,正确的是 (
A.全等三角形的面积相等
B.面积相等的三角形都是全等三角形
C.等边三角形都是面积相等的三角形
D.面积相等的直角三角形都是全等直角三角形
A
)A.全等三角形的面积相等
B.面积相等的三角形都是全等三角形
C.等边三角形都是面积相等的三角形
D.面积相等的直角三角形都是全等直角三角形
答案:A
解析:
A. 对于全等三角形,由于它们的三边及三角都相等,因此它们的面积也必然相等。所以A选项正确。
B. 面积相等的三角形并不意味着它们的三边和三角都相等。例如,底相同、高相同但其他边不相同的两个三角形面积相等,但它们并不全等。所以B选项错误。
C. 等边三角形仅仅说明三角形的三边相等,但并不意味着所有等边三角形的面积都相等。因为面积还取决于三角形的高,而等边三角形的高可以因边长的不同而不同。所以C选项错误。
D. 面积相等的直角三角形仅仅说明它们的面积相同,但并不意味着它们的三边和三角都相等。例如,两个直角三角形,一个的底和高分别为3和4,另一个的底和高分别为2和6,它们的面积都是6,但它们的三边并不相等,因此不全等。所以D选项错误。
B. 面积相等的三角形并不意味着它们的三边和三角都相等。例如,底相同、高相同但其他边不相同的两个三角形面积相等,但它们并不全等。所以B选项错误。
C. 等边三角形仅仅说明三角形的三边相等,但并不意味着所有等边三角形的面积都相等。因为面积还取决于三角形的高,而等边三角形的高可以因边长的不同而不同。所以C选项错误。
D. 面积相等的直角三角形仅仅说明它们的面积相同,但并不意味着它们的三边和三角都相等。例如,两个直角三角形,一个的底和高分别为3和4,另一个的底和高分别为2和6,它们的面积都是6,但它们的三边并不相等,因此不全等。所以D选项错误。
5. 如图,点 A,C,E 在一条直线上,△ABC≌△CDE,试说明:AB//CD.
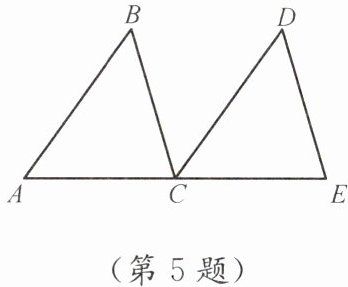

答案:因为$\triangle ABC\cong\triangle CDE$,根据全等三角形的性质,对应角相等,所以$\angle A = \angle DCE$。
因为$\angle A$和$\angle DCE$是内错角,且$\angle A = \angle DCE$,根据内错角相等,两直线平行,所以$AB// CD$。
因为$\angle A$和$\angle DCE$是内错角,且$\angle A = \angle DCE$,根据内错角相等,两直线平行,所以$AB// CD$。
1. 如图,网格中有△ABC 及线段 DE. 请在网格上找一点 F(必须在网格的交点处),使△DEF 与△ABC 全等,这样的点有几个(分别用$ F_1,F_2,F_3,…$表示)?请画出这些三角形.


答案:


解析:
这样的点有4个,分别为$F_1,F_2,F_3,F_4$,画图如下:
(此处需根据网格实际情况画出4个符合条件的点$F_1,F_2,F_3,F_4$及对应的$\triangle DEF_1,\triangle DEF_2,\triangle DEF_3,\triangle DEF_4$)
结论:4个。
(此处需根据网格实际情况画出4个符合条件的点$F_1,F_2,F_3,F_4$及对应的$\triangle DEF_1,\triangle DEF_2,\triangle DEF_3,\triangle DEF_4$)
结论:4个。
2. 如图,△ABE 和△ADC 是△ABC 分别沿着 AB,AC 作轴对称变换得到的. 已知∠1,∠2,∠3 的度数之比为 27∶6∶3,求∠CFE 的度数.


答案:90°
解析:
设∠1=27k,∠2=6k,∠3=3k。
∵∠1+∠2+∠3=180°(三角形内角和定理),
∴27k+6k+3k=180°,解得k=5°。
∴∠1=135°,∠2=30°,∠3=15°。
∵△ABE是△ABC沿AB轴对称得到的,
∴△ABE≌△ABC(轴对称性质),
∴∠ABE=∠ABC=∠2=30°,故∠EBC=∠ABE+∠ABC=30°+30°=60°。
∵△ADC是△ABC沿AC轴对称得到的,
∴△ADC≌△ABC(轴对称性质),
∴∠ACD=∠ACB=∠3=15°,故∠BCD=∠ACB+∠ACD=15°+15°=30°。
在△BFC中,∠BFC=180°-∠FBC-∠FCB=180°-60°-30°=90°。
∵∠CFE与∠BFC是邻补角,
∴∠CFE=180°-∠BFC=180°-90°=90°。
∵∠1+∠2+∠3=180°(三角形内角和定理),
∴27k+6k+3k=180°,解得k=5°。
∴∠1=135°,∠2=30°,∠3=15°。
∵△ABE是△ABC沿AB轴对称得到的,
∴△ABE≌△ABC(轴对称性质),
∴∠ABE=∠ABC=∠2=30°,故∠EBC=∠ABE+∠ABC=30°+30°=60°。
∵△ADC是△ABC沿AC轴对称得到的,
∴△ADC≌△ABC(轴对称性质),
∴∠ACD=∠ACB=∠3=15°,故∠BCD=∠ACB+∠ACD=15°+15°=30°。
在△BFC中,∠BFC=180°-∠FBC-∠FCB=180°-60°-30°=90°。
∵∠CFE与∠BFC是邻补角,
∴∠CFE=180°-∠BFC=180°-90°=90°。