活动一:想一想 说一说
阅读课本第138页的“问题”,回答下列问题:
(1)“问题”中涉及哪些量?哪些量在变化?哪些量没有变化?
(2)第(1)题中的几个量之间有怎样的关系?
阅读课本第138页的“问题”,回答下列问题:
(1)“问题”中涉及哪些量?哪些量在变化?哪些量没有变化?
(2)第(1)题中的几个量之间有怎样的关系?
答案:(1)涉及时间,距离和速度三个量,其中时间和距离是变化的量,速度是不变的量。
(2)距离等于速度乘以时间。
(2)距离等于速度乘以时间。
解析:
(1)在阅读课本第138页的“问题”后,我们可以确定涉及的量主要有时间、距离和速度。其中,时间和距离是随着行驶过程的进行在不断变化的,而速度在题目描述的情境下是保持不变的(假设是匀速行驶)。所以,变化的量是时间和距离,不变的量是速度。
(2)对于第一题中提到的几个量之间的关系,我们可以明确:距离等于速度乘以时间。这是一个基本的运动学公式,描述了匀速直线运动中,物体的行驶距离与其速度和行驶时间的关系。
(2)对于第一题中提到的几个量之间的关系,我们可以明确:距离等于速度乘以时间。这是一个基本的运动学公式,描述了匀速直线运动中,物体的行驶距离与其速度和行驶时间的关系。
活动二:比一比 想一想
阅读课本第138页“围小兔乐园”“购买橘子”内容,并思考:
(1)这两个问题中有哪些量,各个量之间有怎样的关系?
(2)在同一个问题情境中,当一个变量取值确定时,对应的另一个变量是否随之确定?
阅读课本第138页“围小兔乐园”“购买橘子”内容,并思考:
(1)这两个问题中有哪些量,各个量之间有怎样的关系?
(2)在同一个问题情境中,当一个变量取值确定时,对应的另一个变量是否随之确定?
答案:(1)“围小兔乐园”有长、宽、周长,周长固定时长与宽有关系;“购买橘子”有单价、数量、总价,单价固定时总价与数量有关系。(2)是
解析:
(1)“围小兔乐园”中量:长方形的长、宽、周长;关系:周长=2×(长+宽)(周长固定时,长与宽存在关系)。“购买橘子”中量:橘子单价、数量、总价;关系:总价=单价×数量(单价固定时,总价与数量存在关系)。(2)在同一个问题情境中,当一个变量取值确定时,对应的另一个变量随之确定。
活动三:议一议 说一说
你还能举出生活中一些函数的例子吗?借助函数的定义,说说你举的例子为什么是函数.
你还能举出生活中一些函数的例子吗?借助函数的定义,说说你举的例子为什么是函数.
答案:见解析(答案不唯一,合理即可)
解析:
生活中函数的例子很多,比如油箱中剩余油量与行驶时间的关系,当汽车以恒定速度行驶时,随着行驶时间的增加,油箱中的剩余油量会相应减少。在这个关系中,行驶时间是自变量,剩余油量是因变量,对于每一个行驶时间,都对应一个唯一的剩余油量,因此这是一个函数关系。
再比如,一天中某一时刻的气温与该时刻的关系也是一个函数。在一天24小时中,每一个时刻都对应一个特定的气温值,时刻是自变量,气温是因变量,这也满足函数的定义。
以油箱中剩余油量与行驶时间的关系为例,设行驶时间为$t$,剩余油量为$Q$,则对于每一个确定的$t$值,都有一个唯一确定的$Q$值与之对应,这符合函数的定义:设$A,B$是非空的实数集,如果对于集合$A$中的任意一个数$x$,按照某种确定的对应关系$f$,在集合$B$中都有唯一确定的数$y$和它对应,我们就说$f\colon A \to B$是集合$A$到集合$B$的一个函数。
再比如,一天中某一时刻的气温与该时刻的关系也是一个函数。在一天24小时中,每一个时刻都对应一个特定的气温值,时刻是自变量,气温是因变量,这也满足函数的定义。
以油箱中剩余油量与行驶时间的关系为例,设行驶时间为$t$,剩余油量为$Q$,则对于每一个确定的$t$值,都有一个唯一确定的$Q$值与之对应,这符合函数的定义:设$A,B$是非空的实数集,如果对于集合$A$中的任意一个数$x$,按照某种确定的对应关系$f$,在集合$B$中都有唯一确定的数$y$和它对应,我们就说$f\colon A \to B$是集合$A$到集合$B$的一个函数。
1. 如图是刘老师在加油站加油时加油机仪表上某一时刻的数据情况,在加油过程中的常量是 (
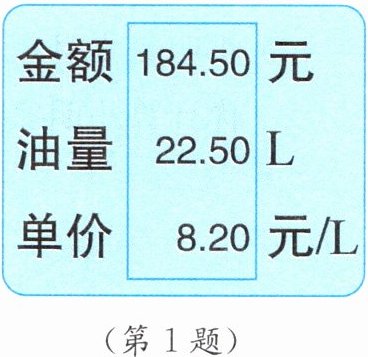
A.金额
B.单价
C.数量
D.金额和数量
B
)
A.金额
B.单价
C.数量
D.金额和数量
答案:B
解析:
在加油过程中,金额会随着加油的数量变化而变化,数量是加油过程中不断增加的变量,而单价在加油过程中保持不变,是一个常量。