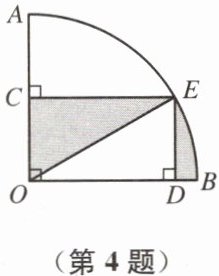
4. 如图,在扇形 AOB 中,$\angle AOB= 90^\circ$,C 是 AO 的中点.过点 C 作$CE\perp AO$垂足为 C,CE 交$\overset{\frown}{AB}$于点 E,过点 E 作$ED\perp OB$,垂足为 D.在扇形 AOB 内任取一点 P,求点 P 落在阴影部分的概率.

答案:$\frac{1}{3}$
解析:
设扇形半径为$r$。
扇形$AOB$面积:$\frac{1}{4}\pi r^2$。
连接$OE$,$OC=\frac{r}{2}$,在$Rt\triangle OCE$中,$\cos\angle COE=\frac{OC}{OE}=\frac{1}{2}$,$\angle COE=60^\circ$,$\angle EOD=30^\circ$。
$CE=\frac{\sqrt{3}}{2}r$,$ED=\frac{r}{2}$,$OD=\frac{\sqrt{3}}{2}r$。
梯形$OCED$面积:$\frac{1}{2}(OC + ED)\cdot OD=\frac{1}{2}(\frac{r}{2}+\frac{r}{2})\cdot\frac{\sqrt{3}}{2}r=\frac{\sqrt{3}}{4}r^2$。
扇形$OCE$面积:$\frac{60^\circ}{360^\circ}\pi r^2=\frac{1}{6}\pi r^2$。
阴影部分面积:梯形$OCED$面积 - 扇形$OCE$面积 + (扇形$OED$面积 - $\triangle OED$面积)。
扇形$OED$面积:$\frac{30^\circ}{360^\circ}\pi r^2=\frac{1}{12}\pi r^2$,$\triangle OED$面积:$\frac{1}{2}OD\cdot ED=\frac{1}{2}\cdot\frac{\sqrt{3}}{2}r\cdot\frac{r}{2}=\frac{\sqrt{3}}{8}r^2$。
经计算阴影部分面积为$\frac{1}{12}\pi r^2$。
概率:$\frac{\frac{1}{12}\pi r^2}{\frac{1}{4}\pi r^2}=\frac{1}{3}$。
$\frac{1}{3}$
扇形$AOB$面积:$\frac{1}{4}\pi r^2$。
连接$OE$,$OC=\frac{r}{2}$,在$Rt\triangle OCE$中,$\cos\angle COE=\frac{OC}{OE}=\frac{1}{2}$,$\angle COE=60^\circ$,$\angle EOD=30^\circ$。
$CE=\frac{\sqrt{3}}{2}r$,$ED=\frac{r}{2}$,$OD=\frac{\sqrt{3}}{2}r$。
梯形$OCED$面积:$\frac{1}{2}(OC + ED)\cdot OD=\frac{1}{2}(\frac{r}{2}+\frac{r}{2})\cdot\frac{\sqrt{3}}{2}r=\frac{\sqrt{3}}{4}r^2$。
扇形$OCE$面积:$\frac{60^\circ}{360^\circ}\pi r^2=\frac{1}{6}\pi r^2$。
阴影部分面积:梯形$OCED$面积 - 扇形$OCE$面积 + (扇形$OED$面积 - $\triangle OED$面积)。
扇形$OED$面积:$\frac{30^\circ}{360^\circ}\pi r^2=\frac{1}{12}\pi r^2$,$\triangle OED$面积:$\frac{1}{2}OD\cdot ED=\frac{1}{2}\cdot\frac{\sqrt{3}}{2}r\cdot\frac{r}{2}=\frac{\sqrt{3}}{8}r^2$。
经计算阴影部分面积为$\frac{1}{12}\pi r^2$。
概率:$\frac{\frac{1}{12}\pi r^2}{\frac{1}{4}\pi r^2}=\frac{1}{3}$。
$\frac{1}{3}$
5. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).小亮随机在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是 4 和 3,求针尖落到小正方形区域(阴影)的概率.


答案:解:∵直角三角形的两条直角边长分别是4和3.
∴直角三角形的斜边长为$ \sqrt {3^2+4^2}=5$
∴大正方形的面积为$ 5^2=25,$
小正方形的面积为$ (4-3)^2=1$
∴P(针尖落在小正方形区域$)=\frac 1{25}$
∴直角三角形的斜边长为$ \sqrt {3^2+4^2}=5$
∴大正方形的面积为$ 5^2=25,$
小正方形的面积为$ (4-3)^2=1$
∴P(针尖落在小正方形区域$)=\frac 1{25}$
解析:
大正方形边长为 $\sqrt{3^2 + 4^2} = 5$,面积为 $5^2 = 25$。
小正方形边长为 $4 - 3 = 1$,面积为 $1^2 = 1$。
针尖落到小正方形区域的概率为 $\frac{1}{25}$。
小正方形边长为 $4 - 3 = 1$,面积为 $1^2 = 1$。
针尖落到小正方形区域的概率为 $\frac{1}{25}$。
6. 阅读:一般地,设试验结果落在某个区域 S 中每一点的机会均等,用 A 表示事件“试验结果落在 S 中的一个小区域 M 中”,那么事件 A 发生的概率$P(A)= \frac{M的面积}{S的面积}$.
问题:如图,在正方形 ABCD 内任取一点 O,连接 OA、OB.如果正方形 ABCD 内每一点被取到的可能性相同,求$\triangle OAB$是直角三角形的概率.
感悟:对于上题的结果,你对“事件的发生”与“事件的概率”有什么新的认识?

问题:如图,在正方形 ABCD 内任取一点 O,连接 OA、OB.如果正方形 ABCD 内每一点被取到的可能性相同,求$\triangle OAB$是直角三角形的概率.
感悟:对于上题的结果,你对“事件的发生”与“事件的概率”有什么新的认识?

答案:解:∵点O在正方形ABCD内且△OAB是直角三角形.
∴∠AOB=90°∴点O在以AB为直径的圆上
∵半圆弧的面积为0
∴ P(△OAB是直角三角形)=0
新的认识∶事件的概率为0并不代表事件不可能发生。
∴∠AOB=90°∴点O在以AB为直径的圆上
∵半圆弧的面积为0
∴ P(△OAB是直角三角形)=0
新的认识∶事件的概率为0并不代表事件不可能发生。
解析:
问题:设正方形边长为$a$,则正方形面积$S = a^2$。$\triangle OAB$是直角三角形时,直角顶点可能为$A$、$B$或$O$。当直角顶点为$A$或$B$时,点$O$分别与$A$、$B$重合,对应区域面积为$0$;当直角顶点为$O$时,点$O$在以$AB$为直径的圆上,该圆在正方形内的部分为一条线段(直径$AB$),面积为$0$。所以事件$A$对应的区域面积$M = 0$,则$P(A)=\frac{M}{S}=\frac{0}{a^2}=0$。
感悟:概率为$0$的事件不一定是不可能事件。
感悟:概率为$0$的事件不一定是不可能事件。