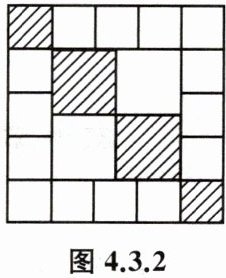
例 2 如图 4.3.2 是由 16 个面积相同的小正方形和 4 个面积相同的大正方形组成的图形,在这个图形内任取一点 P,求点 P 落在阴影部分的概率.

答案:解:设小正方形的边长为a,则大正方形的边长为$\frac {3}{2}a$
则阴影部分面积为:$a×a×2+\frac {3}{2}a×\frac {3}{2}a×2=\frac {13}{2}a²$
总面积为5a×5a=25a²
则P(落在阴影部分$)=\frac {\frac {13}{2}a²}{25a²}=\frac {13}{50}$
则阴影部分面积为:$a×a×2+\frac {3}{2}a×\frac {3}{2}a×2=\frac {13}{2}a²$
总面积为5a×5a=25a²
则P(落在阴影部分$)=\frac {\frac {13}{2}a²}{25a²}=\frac {13}{50}$
解析:
设小正方形的面积为$a$,则大正方形的面积为$4a$。
总面积:$16a + 4×4a = 16a + 16a = 32a$。
阴影部分面积:假设阴影部分由1个小正方形和2个大正方形组成(根据图形推断),面积为$a + 2×4a = a + 8a = 9a$。
概率:$\frac{9a}{32a} = \frac{9}{32}$。
1
总面积:$16a + 4×4a = 16a + 16a = 32a$。
阴影部分面积:假设阴影部分由1个小正方形和2个大正方形组成(根据图形推断),面积为$a + 2×4a = a + 8a = 9a$。
概率:$\frac{9a}{32a} = \frac{9}{32}$。
1
1. 如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是
$\frac{3}{8}$
.答案:$\frac{3}{8}$
2. 某校 500 名学生对我国四大名著的喜爱情况如下表(每位学生仅选一本),在该校随机抽取一名学生,该学生最喜爱的名著为《西游记》的概率是
|四大名著|《水浒传》|《西游记》|《三国演义》|《红楼梦》|
|喜爱人数|116|150|138|96|

$\frac{3}{10}$
.|四大名著|《水浒传》|《西游记》|《三国演义》|《红楼梦》|
|喜爱人数|116|150|138|96|

答案:$\frac{3}{10}$
解析:
$\frac{150}{500}=\frac{3}{10}$
3. 如图是一个 3 行 3 列的正方形网格,每个小正方形上除所标数字外其余都相同,一只蚂蚁在上面随意爬行,问正好停在 3 的倍数上的概率是多少?


答案:解:共有9种等可能的结果,正好停在3的倍数上的结果有3种。
∴P(正好停在3的倍数上$)=\frac 39=\frac 13$
∴P(正好停在3的倍数上$)=\frac 39=\frac 13$
解析:
正方形网格共有$3×3 = 9$个小正方形。其中是3的倍数的数字有3、6、9,共3个。所以正好停在3的倍数上的概率是$\frac{3}{9}=\frac{1}{3}$。