15. 甲、乙、丙三张卡片正面分别写有代数式$a+b$,$2a+b$,$a-b$,这三张卡片除正面的代数式不同外,其余均相同。
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当$a= 1$,$b= -2$时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张。求两次取出的卡片上代数式之和为单项式的概率。
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当$a= 1$,$b= -2$时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张。求两次取出的卡片上代数式之和为单项式的概率。
答案:$(1)$ 求取出的卡片上代数式的值为负数的概率
- **步骤一:分别计算三张卡片上代数式的值
已知$a = 1$,$b=-2$。
对于甲卡片:$a + b=1+( - 2)=1 - 2=-1$;
对于乙卡片:$2a + b=2×1+( - 2)=2 - 2 = 0$;
对于丙卡片:$a - b=1-( - 2)=1 + 2 = 3$。
- **步骤二:根据概率公式计算概率
随机事件概率公式为$P(A)=\frac{m}{n}$,其中$n$是所有可能的结果数,$m$是事件$A$发生的结果数。
这里$n = 3$(三张卡片),$m = 1$(甲卡片的值为负数)。
所以$P=\frac{1}{3}$。
$(2)$ 求两次取出的卡片上代数式之和为单项式的概率
- **步骤一:列出所有可能的结果
根据题意,第一次抽取有$3$种可能,第二次抽取也有$3$种可能,根据分步乘法计数原理,总共有$n = 3×3=9$种可能的结果,分别为$(a + b,a + b)$,$(a + b,2a + b)$,$(a + b,a - b)$,$(2a + b,a + b)$,$(2a + b,2a + b)$,$(2a + b,a - b)$,$(a - b,a + b)$,$(a - b,2a + b)$,$(a - b,a - b)$。
- **步骤二:计算两次代数式之和
$(a + b)+(a + b)=2a + 2b$(多项式);
$(a + b)+(2a + b)=3a + 2b$(多项式);
$(a + b)+(a - b)=2a$(单项式);
$(2a + b)+(a + b)=3a + 2b$(多项式);
$(2a + b)+(2a + b)=4a + 2b$(多项式);
$(2a + b)+(a - b)=3a$(单项式);
$(a - b)+(a + b)=2a$(单项式);
$(a - b)+(2a + b)=3a$(单项式);
$(a - b)+(a - b)=2a-2b$(多项式)。
其中和为单项式的结果有$m = 4$种。
- **步骤三:根据概率公式计算概率
根据概率公式$P(A)=\frac{m}{n}$,这里$n = 9$,$m = 4$,所以$P=\frac{4}{9}$。
综上,答案依次为$(1)$$\boldsymbol{\frac{1}{3}}$;$(2)$$\boldsymbol{\frac{4}{9}}$。
- **步骤一:分别计算三张卡片上代数式的值
已知$a = 1$,$b=-2$。
对于甲卡片:$a + b=1+( - 2)=1 - 2=-1$;
对于乙卡片:$2a + b=2×1+( - 2)=2 - 2 = 0$;
对于丙卡片:$a - b=1-( - 2)=1 + 2 = 3$。
- **步骤二:根据概率公式计算概率
随机事件概率公式为$P(A)=\frac{m}{n}$,其中$n$是所有可能的结果数,$m$是事件$A$发生的结果数。
这里$n = 3$(三张卡片),$m = 1$(甲卡片的值为负数)。
所以$P=\frac{1}{3}$。
$(2)$ 求两次取出的卡片上代数式之和为单项式的概率
- **步骤一:列出所有可能的结果
根据题意,第一次抽取有$3$种可能,第二次抽取也有$3$种可能,根据分步乘法计数原理,总共有$n = 3×3=9$种可能的结果,分别为$(a + b,a + b)$,$(a + b,2a + b)$,$(a + b,a - b)$,$(2a + b,a + b)$,$(2a + b,2a + b)$,$(2a + b,a - b)$,$(a - b,a + b)$,$(a - b,2a + b)$,$(a - b,a - b)$。
- **步骤二:计算两次代数式之和
$(a + b)+(a + b)=2a + 2b$(多项式);
$(a + b)+(2a + b)=3a + 2b$(多项式);
$(a + b)+(a - b)=2a$(单项式);
$(2a + b)+(a + b)=3a + 2b$(多项式);
$(2a + b)+(2a + b)=4a + 2b$(多项式);
$(2a + b)+(a - b)=3a$(单项式);
$(a - b)+(a + b)=2a$(单项式);
$(a - b)+(2a + b)=3a$(单项式);
$(a - b)+(a - b)=2a-2b$(多项式)。
其中和为单项式的结果有$m = 4$种。
- **步骤三:根据概率公式计算概率
根据概率公式$P(A)=\frac{m}{n}$,这里$n = 9$,$m = 4$,所以$P=\frac{4}{9}$。
综上,答案依次为$(1)$$\boldsymbol{\frac{1}{3}}$;$(2)$$\boldsymbol{\frac{4}{9}}$。
16. 甲、乙两位同学相约打乒乓球。
(1)有款式相同的4个乒乓球拍(分别记为A、B、C、D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率。
(2)甲、乙双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球。这个约定是否公平?为什么?
(1)有款式相同的4个乒乓球拍(分别记为A、B、C、D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率。
(2)甲、乙双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球。这个约定是否公平?为什么?
答案:
解:(1)画树状图如下:
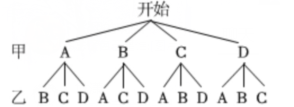
一共有12种等可能的结果,其中乙选择球拍C的结果有3种
所以P(乙选中球拍$C)=\frac {3}{12}=\frac {1}{4}$
(2)画树状图如下:
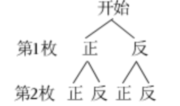
一共4种等可能的结果,其中两枚硬币全部正面向上或全部反面向上的结果有2种
所以P(甲先发球$)=\frac {2}{4}=\frac {1}{2},$所以P(乙先发球$)=1-\frac {1}{2}=\frac {1}{2}$
∵P(甲先发球)=P(乙先发球)
∴这个约定公平
解:(1)画树状图如下:

一共有12种等可能的结果,其中乙选择球拍C的结果有3种
所以P(乙选中球拍$C)=\frac {3}{12}=\frac {1}{4}$
(2)画树状图如下:

一共4种等可能的结果,其中两枚硬币全部正面向上或全部反面向上的结果有2种
所以P(甲先发球$)=\frac {2}{4}=\frac {1}{2},$所以P(乙先发球$)=1-\frac {1}{2}=\frac {1}{2}$
∵P(甲先发球)=P(乙先发球)
∴这个约定公平
17. 在5张相同的小纸条上,分别写有语句:① 函数表达式为$y= x$;② 函数表达式为$y= x^2$;③ 函数的图像关于原点对称;④ 函数的图像关于y轴对称;⑤ 函数值y随自变量x的增大而增大。将这5张小纸条做成5支签,①、②放在不透明的盒子A中搅匀,③、④、⑤放在不透明的盒子B中搅匀。
(1)从盒子A中任意抽出1支签,抽到①概率是______。
(2)先从盒子A中任意抽出1支签,再从盒子B中任意抽出1支签。求抽到的2张小纸条上的语句对函数的描述相符合的概率。
(1)从盒子A中任意抽出1支签,抽到①概率是______。
(2)先从盒子A中任意抽出1支签,再从盒子B中任意抽出1支签。求抽到的2张小纸条上的语句对函数的描述相符合的概率。
答案:
$\frac{1}{2}$
解:(2)列表如下:
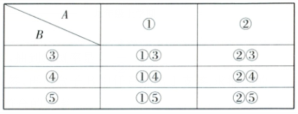
由表可知,共有6种等可能的结果,其中抽到的2张小纸条上的语句对丽数的描述
相符合的结果有①③,①⑤,②④,共3种,
所以抽到的2张小纸条上的语句对函数的描述相符合的概率为$\frac {3}{6}=\frac {1}{2}.$
$\frac{1}{2}$
解:(2)列表如下:

由表可知,共有6种等可能的结果,其中抽到的2张小纸条上的语句对丽数的描述
相符合的结果有①③,①⑤,②④,共3种,
所以抽到的2张小纸条上的语句对函数的描述相符合的概率为$\frac {3}{6}=\frac {1}{2}.$