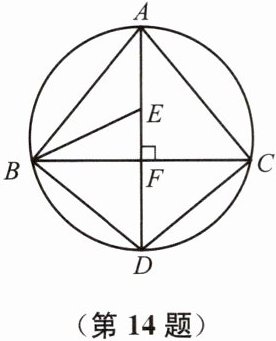
14. (本题10分)如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为F,∠ABC的平分线交AD于点E,连接BD、CD.
(1) 求证:BD= CD.
(2) 请判断B、E、C三点是否都在以点D为圆心,DB为半径的圆上?并说明理由.
(1) 求证:BD= CD.
(2) 请判断B、E、C三点是否都在以点D为圆心,DB为半径的圆上?并说明理由.

答案:证明:( 1 ) :∵AD为△ABC外接圆的直径且AD⊥BC
∴$\overset{\LARGE{ \frown}}{BD}=\overset{\LARGE{ \frown}}{CD}$
∴BD=CD
(2)解:B、E、C都在以点D为圆心,DB为半径的圆上,
理由如下:
∵$\overset{\LARGE{ \frown}}{BD}=\overset{\LARGE{ \frown}}{CD}$
∴∠BAD=∠CBD
∵BE是∠ABC的角平分线
∴∠CBE=∠ABE
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE
∴∠DBE=∠DEB∴DB=DE
∵BD=CD∴DB=DE=CD
∴B,E,C三点在以D为圆心,DB为半径的圆上.
∴$\overset{\LARGE{ \frown}}{BD}=\overset{\LARGE{ \frown}}{CD}$
∴BD=CD
(2)解:B、E、C都在以点D为圆心,DB为半径的圆上,
理由如下:
∵$\overset{\LARGE{ \frown}}{BD}=\overset{\LARGE{ \frown}}{CD}$
∴∠BAD=∠CBD
∵BE是∠ABC的角平分线
∴∠CBE=∠ABE
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE
∴∠DBE=∠DEB∴DB=DE
∵BD=CD∴DB=DE=CD
∴B,E,C三点在以D为圆心,DB为半径的圆上.
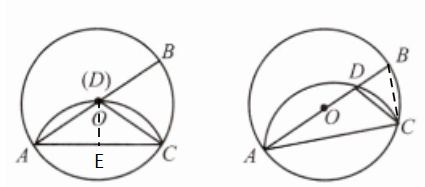
15. (本题10分)在⊙O中,AB为直径,点C在圆上,将劣弧AC沿弦AC翻折交AB于点D,连接CD.
(1) 如图①,若点D与圆心O重合,AC= 2,求⊙O的半径r;
(2) 如图②,若点D与圆心O不重合,∠BAC= 25°,求∠DCA的度数.

(1) 如图①,若点D与圆心O重合,AC= 2,求⊙O的半径r;
(2) 如图②,若点D与圆心O不重合,∠BAC= 25°,求∠DCA的度数.

答案:
解:( 1 ) 过点O作OE⊥AC,垂足为点E,
∵OE⊥AC,AC=2
∴$AE=\frac {1}{2}AC=1$
∵点D翻折后与点O重合
∴$OE=\frac {1}{2}r$
在Rt△OAE中,$OA^2=OE^2+AE^2,$
即$ r^2=(\frac {1}{2}r)^2+1^2$
解得,$r=\frac {2\sqrt{3}}{3}$
∴$\odot O$的半径r为$\frac {2\sqrt{3}}{3}$
( 2 ) 连接BC,∵AB为$\odot O$的直径
∴∠ACB=90°∵∠BAC=25°
∴∠ABC=90°-25°=65°
∵∠ADC是优弧AC所对的圆周角,∠ABC是劣弧AC所对的圆周角
∴∠ADC+∠ABC=180°
∴∠ADC=180°-65°=115°
∴∠BCD=∠ADC-∠ABC=50°
∴∠DCA=90°-∠BCD=40°
解:( 1 ) 过点O作OE⊥AC,垂足为点E,
∵OE⊥AC,AC=2
∴$AE=\frac {1}{2}AC=1$
∵点D翻折后与点O重合
∴$OE=\frac {1}{2}r$
在Rt△OAE中,$OA^2=OE^2+AE^2,$
即$ r^2=(\frac {1}{2}r)^2+1^2$
解得,$r=\frac {2\sqrt{3}}{3}$
∴$\odot O$的半径r为$\frac {2\sqrt{3}}{3}$
( 2 ) 连接BC,∵AB为$\odot O$的直径
∴∠ACB=90°∵∠BAC=25°
∴∠ABC=90°-25°=65°
∵∠ADC是优弧AC所对的圆周角,∠ABC是劣弧AC所对的圆周角
∴∠ADC+∠ABC=180°
∴∠ADC=180°-65°=115°
∴∠BCD=∠ADC-∠ABC=50°
∴∠DCA=90°-∠BCD=40°
