9. 边长为a的正六边形的内切圆的半径为
$\frac{\sqrt{3}}{2}a$
.答案:$\frac{\sqrt{3}}{2}a$
解析:
连接正六边形的中心与任意两个相邻顶点,形成一个等边三角形,其边长为$a$。正六边形内切圆的半径即为该等边三角形的高。根据等边三角形高的计算公式,高$h = \frac{\sqrt{3}}{2} ×$边长,所以内切圆半径为$\frac{\sqrt{3}}{2}a$。
$\frac{\sqrt{3}}{2}a$
$\frac{\sqrt{3}}{2}a$
10. 如图,两正方形彼此相邻且内接于半圆,小正方形的面积为$16 cm^2,$该半圆的半径为______
$4 \sqrt{5} cm$
.答案:$4 \sqrt{5} cm$
解析:
设半圆的圆心为$O$,半径为$r$,小正方形边长为$a$,大正方形边长为$b$。
小正方形面积为$16\ cm^2$,则$a^2 = 16$,$a = 4\ cm$。
连接圆心与大正方形右上顶点,由勾股定理得$r^2 = b^2 + \left(\frac{b}{2}\right)^2$;连接圆心与小正方形右上顶点,得$r^2 = a^2 + \left(\frac{b}{2} + a\right)^2$。
将$a = 4$代入,联立方程:
$\begin{cases}r^2 = b^2 + \frac{b^2}{4} = \frac{5b^2}{4} \\r^2 = 16 + \left(\frac{b}{2} + 4\right)^2\end{cases}$
解得$b = 8$,则$r^2 = \frac{5× 64}{4} = 80$,$r = 4\sqrt{5}\ cm$。
$4\sqrt{5}\ cm$
小正方形面积为$16\ cm^2$,则$a^2 = 16$,$a = 4\ cm$。
连接圆心与大正方形右上顶点,由勾股定理得$r^2 = b^2 + \left(\frac{b}{2}\right)^2$;连接圆心与小正方形右上顶点,得$r^2 = a^2 + \left(\frac{b}{2} + a\right)^2$。
将$a = 4$代入,联立方程:
$\begin{cases}r^2 = b^2 + \frac{b^2}{4} = \frac{5b^2}{4} \\r^2 = 16 + \left(\frac{b}{2} + 4\right)^2\end{cases}$
解得$b = 8$,则$r^2 = \frac{5× 64}{4} = 80$,$r = 4\sqrt{5}\ cm$。
$4\sqrt{5}\ cm$
11. 如图,在△ABC中,∠C= 90°,AC= 8,AB= 10,点P在AC上,AP= 2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是______
1
.答案:1
解析:
在△ABC中,∠C=90°,AC=8,AB=10,由勾股定理得BC=√(AB²-AC²)=√(10²-8²)=6。AP=2,故PC=AC-AP=6。
设⊙O半径为r,圆心O在BP上,过O作OD⊥AC于D,OE⊥AB于E,则OD=OE=r,OD//BC。
PC=BC=6,故△BCP为等腰直角三角形,∠BPC=45°,△ODP为等腰直角三角形,PD=OD=r,OP=√2r。
AD=AP+PD=2+r,点O坐标为(r+2, r)。
直线AB:过点A(8,0)、B(0,6),方程为3x+4y=24。
点O(r+2, r)在直线AB上,代入得3(r+2)+4r=24,解得r=1。
1
设⊙O半径为r,圆心O在BP上,过O作OD⊥AC于D,OE⊥AB于E,则OD=OE=r,OD//BC。
PC=BC=6,故△BCP为等腰直角三角形,∠BPC=45°,△ODP为等腰直角三角形,PD=OD=r,OP=√2r。
AD=AP+PD=2+r,点O坐标为(r+2, r)。
直线AB:过点A(8,0)、B(0,6),方程为3x+4y=24。
点O(r+2, r)在直线AB上,代入得3(r+2)+4r=24,解得r=1。
1
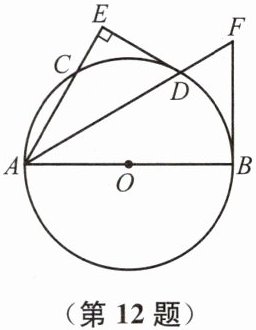
12. (本题10分)如图,AB为⊙O的直径,AD平分∠BAC且交⊙O于点D,DE⊥AC,并交AC的延长线于点E,FB是⊙O的切线,交AD的延长线于点F.
(1) DE是⊙O的切线吗?为什么?
(2) 已知DE= 4,⊙O的半径为5,求AC的长.
(1) DE是⊙O的切线吗?为什么?
(2) 已知DE= 4,⊙O的半径为5,求AC的长.

答案:
解:(1)DE是圆O的切线,理由:如图,连接OD
因为OA= OD所以∠2=∠3
因为AD平分∠BAC所以∠1=∠2
所以∠1=∠3
因为OD//AC,DE⊥AC
所以OD⊥DE
因为OD是圆O的半径
所以DE是圆O的切线.
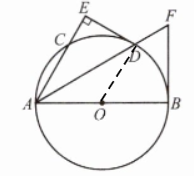
解:( 2 ) 过点D作DP⊥AB。连接CD
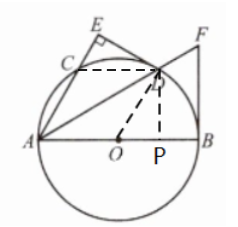
因为AD平分∠BAC,
DE⊥AC,DP⊥AB,DE=4
所以DP=DE=4,
∠AED=∠APD=90°
因为OA=OD
所以OP²=OD²-DP²=9
所以OP=3
所以AP=OA+OP=8
因为∠AED=∠APD=90°,
AD=AD,DE=DP
所以△AED≌△APD
所以AE=AP=8
因为DE是圆O的切线
∴∠EDC=∠EAD
又∠E=∠E
∴△CED∽△DEA
∴$\frac {DE}{CE}=\frac {AE}{DE}$
所以DE²=AE×CE
所以$CE=\frac{DE²}{AE}=2$
所以AC=AE-CE=8-2=6
解:(1)DE是圆O的切线,理由:如图,连接OD
因为OA= OD所以∠2=∠3
因为AD平分∠BAC所以∠1=∠2
所以∠1=∠3
因为OD//AC,DE⊥AC
所以OD⊥DE
因为OD是圆O的半径
所以DE是圆O的切线.

解:( 2 ) 过点D作DP⊥AB。连接CD

因为AD平分∠BAC,
DE⊥AC,DP⊥AB,DE=4
所以DP=DE=4,
∠AED=∠APD=90°
因为OA=OD
所以OP²=OD²-DP²=9
所以OP=3
所以AP=OA+OP=8
因为∠AED=∠APD=90°,
AD=AD,DE=DP
所以△AED≌△APD
所以AE=AP=8
因为DE是圆O的切线
∴∠EDC=∠EAD
又∠E=∠E
∴△CED∽△DEA
∴$\frac {DE}{CE}=\frac {AE}{DE}$
所以DE²=AE×CE
所以$CE=\frac{DE²}{AE}=2$
所以AC=AE-CE=8-2=6
13. (本题10分)如图,△ABC与△ADE都是等腰直角三角形,∠ACB和∠E都是直角,点C在AD上,把△ABC绕点A按顺时针方向旋转后恰好与△ADE重合.若BC= √2,试求线段BC在上述旋转过程中所扫过部分的面积.


答案:解:∵△ABC是等腰三角形,$BC=\sqrt{2}$
∴$AC=\sqrt{2},$AB=2,∠DAB=45°
∵△ABC旋转后与△ADE重合
∴S_{△ABC}=S_{△ADE},AB=AD=2,
$AC=AE=\sqrt{2},$∠CAE=∠DAB=45°
∴S_{阴影部分}=S_{扇形BAD}-S_{△ABC}+S_{△ADE}-S_{扇形CAE}
=S_{扇形BAD}-S_{扇形CAE}
$=\frac {45\pi ×2^2}{360}-\frac {45\pi ×( \sqrt{2} ) ^2}{360}$
$=\frac {\pi}{4}$
∴线段BC在上述旋转过程中所扫过的面积为$\frac {\pi}{4}.$
∴$AC=\sqrt{2},$AB=2,∠DAB=45°
∵△ABC旋转后与△ADE重合
∴S_{△ABC}=S_{△ADE},AB=AD=2,
$AC=AE=\sqrt{2},$∠CAE=∠DAB=45°
∴S_{阴影部分}=S_{扇形BAD}-S_{△ABC}+S_{△ADE}-S_{扇形CAE}
=S_{扇形BAD}-S_{扇形CAE}
$=\frac {45\pi ×2^2}{360}-\frac {45\pi ×( \sqrt{2} ) ^2}{360}$
$=\frac {\pi}{4}$
∴线段BC在上述旋转过程中所扫过的面积为$\frac {\pi}{4}.$
解析:
∵△ABC与△ADE都是等腰直角三角形,∠ACB=∠E=90°,BC=√2,
∴AC=BC=√2,∠BAC=45°,
由勾股定理得AB=√(AC²+BC²)=√((√2)²+(√2)²)=2,
∵△ABC绕点A顺时针旋转后与△ADE重合,
∴旋转角为∠BAD=∠BAC=45°,
线段BC扫过部分的面积为扇形BAD的面积,
S= (45°π×AB²)/360° = (45°π×2²)/360° = π/4 。