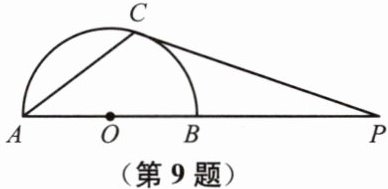
9. 如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.已知∠CPA= 20°,则∠A= ______°.

35
答案:35
解析:
连接OC。
∵PC切半圆O于点C,
∴OC⊥PC,∠OCP=90°。
∵∠CPA=20°,
∴∠COP=90°-20°=70°。
∵OA=OC,
∴∠A=∠OCA。
∵∠COP=∠A+∠OCA=2∠A,
∴∠A=70°÷2=35°。
35
∵PC切半圆O于点C,
∴OC⊥PC,∠OCP=90°。
∵∠CPA=20°,
∴∠COP=90°-20°=70°。
∵OA=OC,
∴∠A=∠OCA。
∵∠COP=∠A+∠OCA=2∠A,
∴∠A=70°÷2=35°。
35
10. 已知圆锥的底面周长是10π,其侧面展开后所得扇形的圆心角为90°,则该圆锥的母线长是______
20
.答案:20
解析:
设圆锥的母线长为$ l $。
圆锥底面周长为$ 10\pi $,侧面展开图扇形的弧长等于底面周长,即弧长$ = 10\pi $。
扇形圆心角为$ 90^\circ $,根据扇形弧长公式$ \frac{n\pi l}{180} $($ n $为圆心角度数),可得:
$ \frac{90\pi l}{180} = 10\pi $
化简得:$ \frac{\pi l}{2} = 10\pi $
两边同时除以$ \pi $:$ \frac{l}{2} = 10 $
解得:$ l = 20 $
20
圆锥底面周长为$ 10\pi $,侧面展开图扇形的弧长等于底面周长,即弧长$ = 10\pi $。
扇形圆心角为$ 90^\circ $,根据扇形弧长公式$ \frac{n\pi l}{180} $($ n $为圆心角度数),可得:
$ \frac{90\pi l}{180} = 10\pi $
化简得:$ \frac{\pi l}{2} = 10\pi $
两边同时除以$ \pi $:$ \frac{l}{2} = 10 $
解得:$ l = 20 $
20
11. 已知一组数据3,a,4,6,7,它们的平均数是5,这组数据的方差是______
2
.答案:2
解析:
$\because$ 数据3,a,4,6,7的平均数是5,$\therefore \frac{3+a+4+6+7}{5}=5$,解得$a=5$。
方差$s^2=\frac{1}{5}[(3-5)^2+(5-5)^2+(4-5)^2+(6-5)^2+(7-5)^2]=\frac{1}{5}[(-2)^2+0^2+(-1)^2+1^2+2^2]=\frac{1}{5}(4+0+1+1+4)=2$。
2
方差$s^2=\frac{1}{5}[(3-5)^2+(5-5)^2+(4-5)^2+(6-5)^2+(7-5)^2]=\frac{1}{5}[(-2)^2+0^2+(-1)^2+1^2+2^2]=\frac{1}{5}(4+0+1+1+4)=2$。
2
12. 如图,将一个球放在一个透明圆柱形玻璃瓶上,测得瓶高AB= 20cm,玻璃瓶底面直径BC= 16cm,球的最高点到玻璃瓶底面的距离为36cm,则球的半径为
10
cm.(玻璃瓶厚度忽略不计)答案:10
解析:
设球的半径为$r$cm。
球的最高点到玻璃瓶底面距离为36cm,瓶高$AB=20$cm,故球心到瓶顶$A$的距离为$(36 - 20 - r)=(16 - r)$cm。
玻璃瓶底面直径$BC=16$cm,半径为8cm,即球心到圆柱底面圆心的水平距离为8cm。
由勾股定理得:$r^2 = 8^2 + (16 - r)^2$。
展开得:$r^2 = 64 + 256 - 32r + r^2$。
化简得:$32r = 320$,解得$r = 10$。
10
球的最高点到玻璃瓶底面距离为36cm,瓶高$AB=20$cm,故球心到瓶顶$A$的距离为$(36 - 20 - r)=(16 - r)$cm。
玻璃瓶底面直径$BC=16$cm,半径为8cm,即球心到圆柱底面圆心的水平距离为8cm。
由勾股定理得:$r^2 = 8^2 + (16 - r)^2$。
展开得:$r^2 = 64 + 256 - 32r + r^2$。
化简得:$32r = 320$,解得$r = 10$。
10
13. (本题8分)解下列方程:
$(1) 4(x+3)^2-16= 0;$
$(2) (x+3)^2= 5(x+3).$
$(1) 4(x+3)^2-16= 0;$
$(2) (x+3)^2= 5(x+3).$
答案:解:$4x^2+24x+20=0$
$x^2+6x+5=0$
(x+1)(x+5)=0
x+1=0或x+5=0
$x_1=-1,$$x_2=-5$
解:$(x+3)^2-5(x+3)=0$
(x+3)(x+3-5)=0
x+3=0或x+3-5=0
$x_1=-3,$$x_2=2$
$x^2+6x+5=0$
(x+1)(x+5)=0
x+1=0或x+5=0
$x_1=-1,$$x_2=-5$
解:$(x+3)^2-5(x+3)=0$
(x+3)(x+3-5)=0
x+3=0或x+3-5=0
$x_1=-3,$$x_2=2$
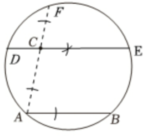
14. (本题6分)如图,点C为圆内一点,AB为该圆的一条弦.
(1) 请在图①中用无刻度的直尺和圆规作图:过点C作直线l与AB平行,分别交该圆于点D、E(点D在点E的左侧);(不写作法,保留作图痕迹)
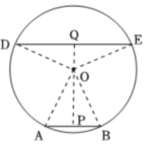
(2) 在(1)中,若AB与DE位于圆心异侧,且AB= 2,DE= 4$\sqrt{2}$,已知该圆的半径为3,则该圆位于AB和DE之间的图形的面积为______.(如需画草图,请使用图②)

(1) 请在图①中用无刻度的直尺和圆规作图:过点C作直线l与AB平行,分别交该圆于点D、E(点D在点E的左侧);(不写作法,保留作图痕迹)
(2) 在(1)中,若AB与DE位于圆心异侧,且AB= 2,DE= 4$\sqrt{2}$,已知该圆的半径为3,则该圆位于AB和DE之间的图形的面积为______.(如需画草图,请使用图②)

答案:
$\frac {9π}{2}+4\sqrt{2}$
$\frac {9π}{2}+4\sqrt{2}$

