19. (本题8分)某校为了让学生在课间有足够的活动空间,常设法充分利用走廊、平台、小广场、转角等"金角银边".该校有一块长为21m、宽为10m的矩形小广场,计划在其中打造两块相同的运动区域,两块运动区域之间及周边留有宽度相等的人行通道,且人行通道的宽度不超过3m.
(1) 如果两块运动区域的面积之和为$90m^2,$求人行通道的宽度.
(2) 能否改变人行通道的宽度,使得每块运动区域的宽与长之比等于3:5?请说明理由.

(1) 如果两块运动区域的面积之和为$90m^2,$求人行通道的宽度.
(2) 能否改变人行通道的宽度,使得每块运动区域的宽与长之比等于3:5?请说明理由.

答案:1. (1)
设人行通道的宽度为$x$米。
已知矩形小广场长为$21$米、宽为$10$米,那么两块运动区域拼在一起,长为$(21 - 3x)$米,宽为$(10 - 2x)$米。
根据两块运动区域的面积之和为$90m^{2}$,可列方程$(21 - 3x)(10 - 2x)=90$。
展开括号得:$210-42x - 30x+6x^{2}=90$。
移项化为一元二次方程的一般形式:$6x^{2}-72x + 120 = 0$,两边同时除以$6$得$x^{2}-12x + 20 = 0$。
分解因式:$(x - 10)(x - 2)=0$。
则$x - 10 = 0$或$x - 2 = 0$,解得$x_{1}=10$,$x_{2}=2$。
因为人行通道的宽度不超过$3$米,而$x = 10$不符合题意,舍去。
所以人行通道的宽度为$2$米。
2. (2)
设人行通道的宽度为$y$米。
若每块运动区域的宽与长之比等于$3:5$,则$\frac{10 - 2y}{21 - 3y}=\frac{3}{5}$。
交叉相乘得:$5(10 - 2y)=3(21 - 3y)$。
展开括号:$50-10y = 63 - 9y$。
移项:$-10y + 9y=63 - 50$。
解得$y=-13$。
因为$y=-13$不符合实际意义(宽度不能为负),所以不能改变人行通道的宽度,使得每块运动区域的宽与长之比等于$3:5$。
综上,(1)人行通道的宽度为$2$米;(2)不能,理由如上述步骤。
设人行通道的宽度为$x$米。
已知矩形小广场长为$21$米、宽为$10$米,那么两块运动区域拼在一起,长为$(21 - 3x)$米,宽为$(10 - 2x)$米。
根据两块运动区域的面积之和为$90m^{2}$,可列方程$(21 - 3x)(10 - 2x)=90$。
展开括号得:$210-42x - 30x+6x^{2}=90$。
移项化为一元二次方程的一般形式:$6x^{2}-72x + 120 = 0$,两边同时除以$6$得$x^{2}-12x + 20 = 0$。
分解因式:$(x - 10)(x - 2)=0$。
则$x - 10 = 0$或$x - 2 = 0$,解得$x_{1}=10$,$x_{2}=2$。
因为人行通道的宽度不超过$3$米,而$x = 10$不符合题意,舍去。
所以人行通道的宽度为$2$米。
2. (2)
设人行通道的宽度为$y$米。
若每块运动区域的宽与长之比等于$3:5$,则$\frac{10 - 2y}{21 - 3y}=\frac{3}{5}$。
交叉相乘得:$5(10 - 2y)=3(21 - 3y)$。
展开括号:$50-10y = 63 - 9y$。
移项:$-10y + 9y=63 - 50$。
解得$y=-13$。
因为$y=-13$不符合实际意义(宽度不能为负),所以不能改变人行通道的宽度,使得每块运动区域的宽与长之比等于$3:5$。
综上,(1)人行通道的宽度为$2$米;(2)不能,理由如上述步骤。
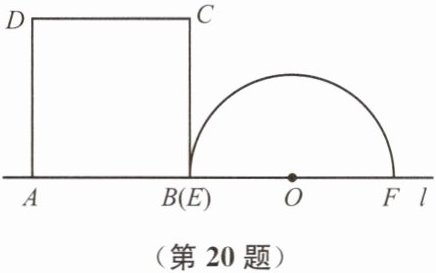
20. (本题8分)如图,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB= 7,EF= 10,BC>5.点B以1个单位长度每秒的速度从点E处出发,沿射线EF方向运动,矩形ABCD随之运动,运动时间为ts.
(1) 求当t= 2.5时半圆O在矩形ABCD内的弧的长度.
(2) 在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H.连接OG、OH.若∠GOH为直角,求此时t的值.
(1) 求当t= 2.5时半圆O在矩形ABCD内的弧的长度.
(2) 在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H.连接OG、OH.若∠GOH为直角,求此时t的值.

答案:
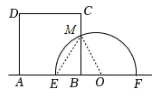
解:(1)设BC与⊙O交于点M,当t=2.5时,BE=2.5,
∵EF=10,∴$OE=\frac {1}{2}EF=5,$
∴OB=2.5,∴EB=OB,
在矩形ABCD中,∠ABC=90°,∴ME=MO,
又∵MO=EO,∴ME=EO=MO,
∴△MOE是等边三角形,∴∠EOM=60°,
∴$l_{ME}=\frac {60π×5}{180}=\frac {5π}{3}.$
∴半圆O在矩形ABCD内的弧的长度为$\frac {5π}{3}.$
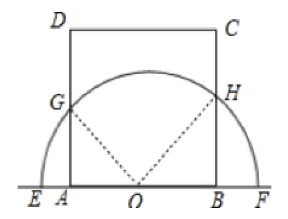
(2)连接GO,HO,∵∠GOH=90°,∴∠AOG+∠BOH=90°,
∵∠AGO+∠AOG=90°,∴∠AGO=∠BOH,
在△AGO和△OBH中,
$\begin{cases}∠AGO=∠BOH\\∠GAO=∠HBO\\OG=OH\end{cases}$
∴$△AGO≌△BOH(\mathrm {AAS}),$
∴OB=AG=t-5,∵AB=7,∴AE=t-7,
∴AO=5-(t-7)=12-t,在Rt△AGO中,$AG^2+AO^2=OG^2,$
∴$(t-5)^2+(12-t)^2=5^2,$
解得:$t_1=8,$$t_2=9,$即t的值为8或9.
解:(1)设BC与⊙O交于点M,当t=2.5时,BE=2.5,
∵EF=10,∴$OE=\frac {1}{2}EF=5,$
∴OB=2.5,∴EB=OB,
在矩形ABCD中,∠ABC=90°,∴ME=MO,
又∵MO=EO,∴ME=EO=MO,
∴△MOE是等边三角形,∴∠EOM=60°,
∴$l_{ME}=\frac {60π×5}{180}=\frac {5π}{3}.$
∴半圆O在矩形ABCD内的弧的长度为$\frac {5π}{3}.$
(2)连接GO,HO,∵∠GOH=90°,∴∠AOG+∠BOH=90°,
∵∠AGO+∠AOG=90°,∴∠AGO=∠BOH,
在△AGO和△OBH中,
$\begin{cases}∠AGO=∠BOH\\∠GAO=∠HBO\\OG=OH\end{cases}$
∴$△AGO≌△BOH(\mathrm {AAS}),$
∴OB=AG=t-5,∵AB=7,∴AE=t-7,
∴AO=5-(t-7)=12-t,在Rt△AGO中,$AG^2+AO^2=OG^2,$
∴$(t-5)^2+(12-t)^2=5^2,$
解得:$t_1=8,$$t_2=9,$即t的值为8或9.

