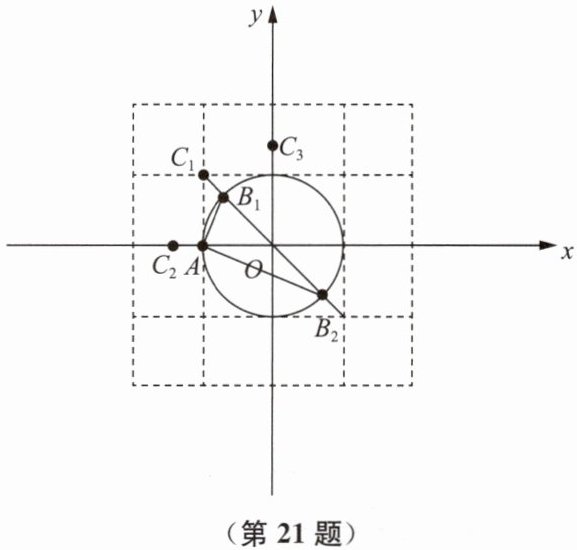
21. (本题8分)如图,在平面直角坐标系中,⊙O的半径为1.对于⊙O的弦AB和⊙O外一点C给出如下定义:若直线CA、CB中一条经过点O,另一条是⊙O的切线,则称点C是弦AB的"关联点".已知点A(-1,0)、B₁(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)、B₂($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
(1) 在点C₁(-1,1)、C₂(-$\sqrt{2}$,0)、C₃(0,$\sqrt{2}$)中,弦AB₁的"关联点"是______.
(2) 若点C是弦AB₂的"关联点",求出点C的坐标.


解：(2)分两种情况
①当AC经过圆心，$B_2C$是⊙O的切线时
此时$B_2C⊥B_2O$
∵$B_2(\frac {\sqrt{2}}{2}，－\frac {\sqrt{2}}{2})$
∴$y_{B_2O}=－x$
∴直线$B_2C$的斜率为1
设直线$B_2C$的解析式为y=x+b
把$(\frac {\sqrt{2}}{2}，－\frac {\sqrt{2}}{2})$代入：
$\frac {\sqrt{2}}{2}+b=－\frac {\sqrt{2}}{2}$
$b=－\sqrt{2}，$∴$y_{B_2C}=x－\sqrt{2}$
当y=0时，$x－\sqrt{2}=0，x=\sqrt{2}$
∴$C(\sqrt{2}，0)$
②当$B_2C$经过圆心，AC是⊙O的切线时
∵A(－1,0)∴C的横坐标为－1
由①知，直线$B_2O$的解析式为y=－x
当x=－1时，y=1
∴C(－1，1)
综上所述：$C(\sqrt{2}，0)$或(－1,1)