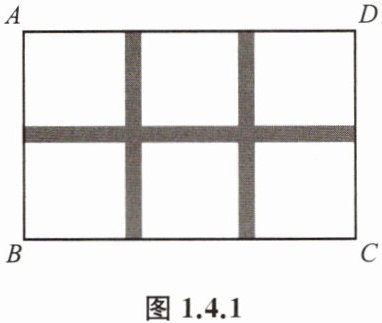
例2 如图1.4.1,在宽为20 m、长为32 m的矩形耕地上修建同样宽的三条道路(横向与纵向垂直),耕地被道路分成若干个小矩形块作为小麦试验田.假设试验田面积为$570 m^2,$求道路的宽.

答案:解:设道路的宽度是x米.
依题意得
(20-x)(32-2x)=570
解得x=1或x=35(不合题意,舍去)
答:道路的宽是1米.
依题意得
(20-x)(32-2x)=570
解得x=1或x=35(不合题意,舍去)
答:道路的宽是1米.
解析:
设道路的宽为$x\ m$。
根据题意,横向道路面积为$32x\ m^2$,纵向道路面积为$2×20x\ m^2$,重叠部分面积为$2x^2\ m^2$,耕地总面积为$32×20 = 640\ m^2$,试验田面积为$570\ m^2$,则可列方程:
$640-(32x + 2×20x - 2x^2)=570$
化简得:
$2x^2 - 72x + 70 = 0$
$x^2 - 36x + 35 = 0$
因式分解:
$(x - 1)(x - 35)=0$
解得$x_1 = 1$,$x_2 = 35$(因$35>20$,不合题意,舍去)。
道路的宽为$1\ m$。
根据题意,横向道路面积为$32x\ m^2$,纵向道路面积为$2×20x\ m^2$,重叠部分面积为$2x^2\ m^2$,耕地总面积为$32×20 = 640\ m^2$,试验田面积为$570\ m^2$,则可列方程:
$640-(32x + 2×20x - 2x^2)=570$
化简得:
$2x^2 - 72x + 70 = 0$
$x^2 - 36x + 35 = 0$
因式分解:
$(x - 1)(x - 35)=0$
解得$x_1 = 1$,$x_2 = 35$(因$35>20$,不合题意,舍去)。
道路的宽为$1\ m$。
1. 从一块正方形的木板上锯掉2 m宽的长方形木条,剩下的面积是$48 m^2,$则原来这块木板的面积是
64m²
.答案:64m²
解析:
设原来正方形木板的边长为$x\ m$。
锯掉$2\ m$宽的长方形木条后,剩下的长方形的长为$x\ m$,宽为$(x - 2)\ m$。
根据剩下的面积是$48\ m^2$,可得方程:$x(x - 2) = 48$
展开方程:$x^2 - 2x - 48 = 0$
因式分解:$(x - 8)(x + 6) = 0$
解得:$x_1 = 8$,$x_2 = -6$(边长不能为负,舍去)
原来正方形木板的面积为:$x^2 = 8^2 = 64\ m^2$
64 m²
锯掉$2\ m$宽的长方形木条后,剩下的长方形的长为$x\ m$,宽为$(x - 2)\ m$。
根据剩下的面积是$48\ m^2$,可得方程:$x(x - 2) = 48$
展开方程:$x^2 - 2x - 48 = 0$
因式分解:$(x - 8)(x + 6) = 0$
解得:$x_1 = 8$,$x_2 = -6$(边长不能为负,舍去)
原来正方形木板的面积为:$x^2 = 8^2 = 64\ m^2$
64 m²
2. 一个两位数,它的个位数字与十位数字之和为9,这两个数字的积等于这个两位数的$\frac{1}{2}$,则这个两位数是__
36
__.答案:36
解析:
设这个两位数的十位数字为$x$,则个位数字为$9 - x$。
这个两位数可表示为$10x + (9 - x) = 9x + 9$。
根据题意,得$x(9 - x) = \frac{1}{2}(9x + 9)$。
整理方程,得$2x(9 - x) = 9x + 9$,即$18x - 2x^2 = 9x + 9$,移项化简为$2x^2 - 9x + 9 = 0$。
因式分解,得$(2x - 3)(x - 3) = 0$,解得$x_1 = 3$,$x_2 = \frac{3}{2}$(不合题意,舍去)。
当$x = 3$时,个位数字为$9 - 3 = 6$,所以这个两位数是$36$。
36
这个两位数可表示为$10x + (9 - x) = 9x + 9$。
根据题意,得$x(9 - x) = \frac{1}{2}(9x + 9)$。
整理方程,得$2x(9 - x) = 9x + 9$,即$18x - 2x^2 = 9x + 9$,移项化简为$2x^2 - 9x + 9 = 0$。
因式分解,得$(2x - 3)(x - 3) = 0$,解得$x_1 = 3$,$x_2 = \frac{3}{2}$(不合题意,舍去)。
当$x = 3$时,个位数字为$9 - 3 = 6$,所以这个两位数是$36$。
36
3. 小明在演算某数的平方时,将这个数的平方误看成它的2倍,使答案少了35,则这个数为
7或-5
.答案:7或-5
解析:
设这个数为$x$。
根据题意,得$x^{2}-2x=35$
整理,得$x^{2}-2x-35=0$
因式分解,得$(x-7)(x+5)=0$
解得$x_{1}=7$,$x_{2}=-5$
7或-5
根据题意,得$x^{2}-2x=35$
整理,得$x^{2}-2x-35=0$
因式分解,得$(x-7)(x+5)=0$
解得$x_{1}=7$,$x_{2}=-5$
7或-5
4. 如图,用长为30 m的篱笆,一面靠墙(墙的最大可用长度为10 m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.如果要围成总面积为$63 m^2$的花圃,那么花圃的宽AB应为多少?


答案: 解:设该花圃的一边AB的长为xm,则与AB相邻的边的
长为$30-3x\ \mathrm {m},$
由题意得:(30-3x)x=63,
即:$x^2-10x+21=0,$
解得:$x_1=3,$$x_2=7$
当x=3m时,平行与墙的一边长为:30-3x=21m>10m,不合题意舍去.
当x=7m时,平行与墙的一边长为:30-3x=9m<10m,符合题意.
所以,AB的长是7m.
长为$30-3x\ \mathrm {m},$
由题意得:(30-3x)x=63,
即:$x^2-10x+21=0,$
解得:$x_1=3,$$x_2=7$
当x=3m时,平行与墙的一边长为:30-3x=21m>10m,不合题意舍去.
当x=7m时,平行与墙的一边长为:30-3x=9m<10m,符合题意.
所以,AB的长是7m.
解析:
设花圃的宽$AB$为$x\ m$,则$BC=(30 - 3x)\ m$。
根据题意,得$x(30 - 3x)=63$,
整理,得$x^{2}-10x + 21=0$,
解得$x_{1}=3$,$x_{2}=7$。
当$x = 3$时,$BC=30-3×3=21\ m$,
$\because21>10$,不符合题意,舍去;
当$x = 7$时,$BC=30-3×7=9\ m$,
$\because9<10$,符合题意。
答:花圃的宽$AB$应为$7\ m$。
根据题意,得$x(30 - 3x)=63$,
整理,得$x^{2}-10x + 21=0$,
解得$x_{1}=3$,$x_{2}=7$。
当$x = 3$时,$BC=30-3×3=21\ m$,
$\because21>10$,不符合题意,舍去;
当$x = 7$时,$BC=30-3×7=9\ m$,
$\because9<10$,符合题意。
答:花圃的宽$AB$应为$7\ m$。