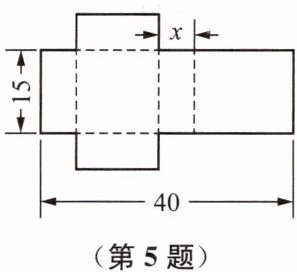
5. 已知一个包装盒的表面展开如图所示.若此包装盒的容积为$1125 cm^3,$请列出关于x的方程,并求出x的值.

答案:解:依题意得
15x(20-x)=1125
解得$x_1=5,$$x_2=15$
15x(20-x)=1125
解得$x_1=5,$$x_2=15$
解析:
由展开图可知,包装盒为长方体,高为$15\ cm$。
若长方体的长为$x\ cm$,则宽为$\frac{40 - 2x}{2} = (20 - x)\ cm$。
根据容积公式$长×宽×高 = 容积$,可得方程:
$15x(20 - x) = 1125$
化简得:
$x(20 - x) = 75$
$20x - x^2 = 75$
$x^2 - 20x + 75 = 0$
因式分解:
$(x - 5)(x - 15) = 0$
解得$x = 5$或$x = 15$。
5 cm或15 cm
若长方体的长为$x\ cm$,则宽为$\frac{40 - 2x}{2} = (20 - x)\ cm$。
根据容积公式$长×宽×高 = 容积$,可得方程:
$15x(20 - x) = 1125$
化简得:
$x(20 - x) = 75$
$20x - x^2 = 75$
$x^2 - 20x + 75 = 0$
因式分解:
$(x - 5)(x - 15) = 0$
解得$x = 5$或$x = 15$。
5 cm或15 cm
6. 如图,某小区有一块长18 m、宽6 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为$60 m^2,$两块绿地之间及周边留有宽度相等的人行通道.求人行通道的宽度.


答案:解:设人行通道的宽度为x米。
依题意得,(18-3x)(6 -2x) =60
解得,$x_1 = 1,$$x_2 =8($不合题意,舍去)
答:人行通道的宽度为1米。
依题意得,(18-3x)(6 -2x) =60
解得,$x_1 = 1,$$x_2 =8($不合题意,舍去)
答:人行通道的宽度为1米。
7. 某小区有一块长100 m、宽80 m的矩形空地,现将其建成如图所示的花园广场,四角的阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,预计活动区造价为60元$/m^2,$绿化区造价为50元$/m^2.$如果小区投资47.2万元,且准备全部用完.设每块绿化区的长边为x m,问能否完成工程任务?若能,请求出x的值;若不能,请说明理由.


答案:解:依题意得
50×4x(x-10)+60×[80×100-4x(x-10)]=472000
解得$x_1=20,$$x_2=-10($舍去)
∴能够完成任务,此时x的值为20.
50×4x(x-10)+60×[80×100-4x(x-10)]=472000
解得$x_1=20,$$x_2=-10($舍去)
∴能够完成任务,此时x的值为20.
解析:
设每块绿化区的短边为$y\ m$,由题意得出口宽度为$2y\ m$,且$100 - 2x = 80 - 2y$,解得$y = x - 10$。
绿化区总面积为$4xy = 4x(x - 10)$,活动区总面积为$100×80 - 4x(x - 10)$。
投资总额为$50×4x(x - 10) + 60×[8000 - 4x(x - 10)] = 472000$,化简得$-40x(x - 10) + 480000 = 472000$,即$x(x - 10) = 200$,$x^2 - 10x - 200 = 0$,解得$x = 20$($x = -10$舍去)。
能完成工程任务,$x = 20$。
绿化区总面积为$4xy = 4x(x - 10)$,活动区总面积为$100×80 - 4x(x - 10)$。
投资总额为$50×4x(x - 10) + 60×[8000 - 4x(x - 10)] = 472000$,化简得$-40x(x - 10) + 480000 = 472000$,即$x(x - 10) = 200$,$x^2 - 10x - 200 = 0$,解得$x = 20$($x = -10$舍去)。
能完成工程任务,$x = 20$。