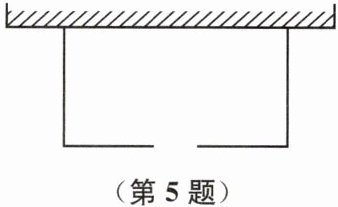
5. 如图,用长32 m的木条围成一个面积为$130m^{2}$的矩形仓库,仓库的一面靠墙(墙宽16 m),在与墙平行的一边开一道1 m宽的门.求垂直于墙的一边长.

答案:解:设垂直于墙的一边长 x 米.
依题意得,x(32+1-2x)=130
解得,$x_1=10,$$x_2=\frac {13}{2},$
当x=10时,32+1-2x=13<16,符合题意;
当$x=\frac {13}{2}$时,32+12x=20>16,不合题意,故舍去.
∴x=10
答:垂直于墙的一边长10米.
依题意得,x(32+1-2x)=130
解得,$x_1=10,$$x_2=\frac {13}{2},$
当x=10时,32+1-2x=13<16,符合题意;
当$x=\frac {13}{2}$时,32+12x=20>16,不合题意,故舍去.
∴x=10
答:垂直于墙的一边长10米.
解析:
设垂直于墙的一边长为$x$ m,则与墙平行的一边长为$(32 - 2x + 1)$ m。
根据题意,得$x(32 - 2x + 1) = 130$,
整理,得$2x^2 - 33x + 130 = 0$,
解得$x_1 = 10$,$x_2 = \frac{13}{2}$。
当$x = 10$时,$32 - 2x + 1 = 13$,$13 < 16$,符合题意;
当$x = \frac{13}{2}$时,$32 - 2x + 1 = 20$,$20 > 16$,不符合题意,舍去。
垂直于墙的一边长为$10$ m。
根据题意,得$x(32 - 2x + 1) = 130$,
整理,得$2x^2 - 33x + 130 = 0$,
解得$x_1 = 10$,$x_2 = \frac{13}{2}$。
当$x = 10$时,$32 - 2x + 1 = 13$,$13 < 16$,符合题意;
当$x = \frac{13}{2}$时,$32 - 2x + 1 = 20$,$20 > 16$,不符合题意,舍去。
垂直于墙的一边长为$10$ m。
6. 某大型水果超市销售水蜜桃,水蜜桃的进价是40元/箱,根据前段时间的销售经验,售价x(元/箱)与销售量y(箱)满足关系:$y= -5x+380$.
(1)若该超市每天销售水蜜桃盈利1 600元,则每箱售价是多少元?
(2)七月份连续阴雨,销售量减少,超市决定降价销售,从7月17日开始,水蜜桃售价在(1)的条件下下降了$m\%$,同时水蜜桃的进价下降了10%,销售量也因此比原来每天盈利1 600元时上涨了$2m\%$$(m<100)$,7月份(按31天计算)降价销售后总盈利比7月份降价销售前的销售总盈利少7 120元,求m的值.
(1)若该超市每天销售水蜜桃盈利1 600元,则每箱售价是多少元?
(2)七月份连续阴雨,销售量减少,超市决定降价销售,从7月17日开始,水蜜桃售价在(1)的条件下下降了$m\%$,同时水蜜桃的进价下降了10%,销售量也因此比原来每天盈利1 600元时上涨了$2m\%$$(m<100)$,7月份(按31天计算)降价销售后总盈利比7月份降价销售前的销售总盈利少7 120元,求m的值.
答案:解:
(1)由题意得:(x-40)(-5x+380)=1600
解得:$x_{1}=56,x_{2}=60$
答:每箱的售价是56元或60元。
(2)在
(1)的条件下,x=56,y=100
由题意:1600×16=[56×(1-m%)-40×(1-10%)]×100×(1+2m%)×15+7120
解得:$m_1=20,$$m_2=-\frac {280}{7}($舍去)
所以m的值为20
(1)由题意得:(x-40)(-5x+380)=1600
解得:$x_{1}=56,x_{2}=60$
答:每箱的售价是56元或60元。
(2)在
(1)的条件下,x=56,y=100
由题意:1600×16=[56×(1-m%)-40×(1-10%)]×100×(1+2m%)×15+7120
解得:$m_1=20,$$m_2=-\frac {280}{7}($舍去)
所以m的值为20
7. 某批发商以每件50元的价格购进800件T恤,第一个月以单价80元售出200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
答案:解:设第二个月的单价应是 x 元.( x>50 )
第二个月的销量:200+10( 80-x ) =1000-10x( 件 )
依题意得,
80×200+x( 1000-10x ) +40[ 800-200-( 1000-10x ) ] =50×800+9000
解得,$x_1=x_2=70$
答:第二个月的单价应是70元.
第二个月的销量:200+10( 80-x ) =1000-10x( 件 )
依题意得,
80×200+x( 1000-10x ) +40[ 800-200-( 1000-10x ) ] =50×800+9000
解得,$x_1=x_2=70$
答:第二个月的单价应是70元.
解析:
设第二个月的单价降低$x$元,则第二个月的单价为$(80 - x)$元,销售量为$(200 + 10x)$件。
第一个月利润:$(80 - 50)×200 = 30×200 = 6000$元。
第二个月利润:$(80 - x - 50)(200 + 10x) = (30 - x)(200 + 10x)$元。
剩余T恤数量:$800 - 200 - (200 + 10x) = 400 - 10x$件。
清仓利润:$(40 - 50)(400 - 10x) = -10(400 - 10x) = -4000 + 100x$元。
总利润为各月利润之和,依题意得:
$6000 + (30 - x)(200 + 10x) + (-4000 + 100x) = 9000$
化简$(30 - x)(200 + 10x)$:
$\begin{aligned}&30×200 + 30×10x - 200x - 10x^2\\=&6000 + 300x - 200x - 10x^2\\=&6000 + 100x - 10x^2\end{aligned}$
代入总利润方程:
$6000 + 6000 + 100x - 10x^2 - 4000 + 100x = 9000$
合并同类项:
$(6000 + 6000 - 4000) + (100x + 100x) - 10x^2 = 9000$
$8000 + 200x - 10x^2 = 9000$
移项整理:
$-10x^2 + 200x + 8000 - 9000 = 0$
$-10x^2 + 200x - 1000 = 0$
两边同除以$-10$:
$x^2 - 20x + 100 = 0$
因式分解:
$(x - 10)^2 = 0$
解得$x = 10$。
第二个月单价:$80 - x = 80 - 10 = 70$元,且$70 > 50$,符合题意。
第二个月的单价应是70元。
第一个月利润:$(80 - 50)×200 = 30×200 = 6000$元。
第二个月利润:$(80 - x - 50)(200 + 10x) = (30 - x)(200 + 10x)$元。
剩余T恤数量:$800 - 200 - (200 + 10x) = 400 - 10x$件。
清仓利润:$(40 - 50)(400 - 10x) = -10(400 - 10x) = -4000 + 100x$元。
总利润为各月利润之和,依题意得:
$6000 + (30 - x)(200 + 10x) + (-4000 + 100x) = 9000$
化简$(30 - x)(200 + 10x)$:
$\begin{aligned}&30×200 + 30×10x - 200x - 10x^2\\=&6000 + 300x - 200x - 10x^2\\=&6000 + 100x - 10x^2\end{aligned}$
代入总利润方程:
$6000 + 6000 + 100x - 10x^2 - 4000 + 100x = 9000$
合并同类项:
$(6000 + 6000 - 4000) + (100x + 100x) - 10x^2 = 9000$
$8000 + 200x - 10x^2 = 9000$
移项整理:
$-10x^2 + 200x + 8000 - 9000 = 0$
$-10x^2 + 200x - 1000 = 0$
两边同除以$-10$:
$x^2 - 20x + 100 = 0$
因式分解:
$(x - 10)^2 = 0$
解得$x = 10$。
第二个月单价:$80 - x = 80 - 10 = 70$元,且$70 > 50$,符合题意。
第二个月的单价应是70元。