9. 如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC= a,EF= b,NH= c.下列各式中,正确的是(
A.a>b>c
B.a= b= c
C.c>a>b
D.b>c>a
B
)A.a>b>c
B.a= b= c
C.c>a>b
D.b>c>a
答案:B
解析:
连接OA、OD、OM。
∵四边形ABOC是矩形,
∴BC=OA。
同理,EF=OD,NH=OM。
∵点A、D、M在半圆O上,
∴OA=OD=OM=半圆半径。
∴BC=EF=NH,即a=b=c。
B.
∵四边形ABOC是矩形,
∴BC=OA。
同理,EF=OD,NH=OM。
∵点A、D、M在半圆O上,
∴OA=OD=OM=半圆半径。
∴BC=EF=NH,即a=b=c。
B.
10. 如图,在⊙O中,直径MN= 10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,且∠POM= 45°.求正方形的边长.
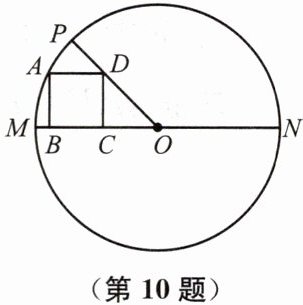

答案:
解∶连接OA,设正方形ABCD的边长为 x
∵正方形ABCD的边长为 x
∴AB=BC=CD=x, ∠OCD=90°.
∴∠POM=45°
∴△OCD为等腰直角三角形,CD=CO=x
∴OB=2x
在Rt△OAB中,
∵AB=x,OB=2x.
∴$OA=\sqrt{5}x$
∵直径MN=10
∴$2\sqrt{5}x=10$
解得,$x=\sqrt{5}$
∴正方形的边长为$\sqrt{5}.$
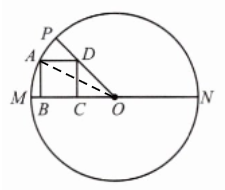
解∶连接OA,设正方形ABCD的边长为 x
∵正方形ABCD的边长为 x
∴AB=BC=CD=x, ∠OCD=90°.
∴∠POM=45°
∴△OCD为等腰直角三角形,CD=CO=x
∴OB=2x
在Rt△OAB中,
∵AB=x,OB=2x.
∴$OA=\sqrt{5}x$
∵直径MN=10
∴$2\sqrt{5}x=10$
解得,$x=\sqrt{5}$
∴正方形的边长为$\sqrt{5}.$

解析:
设正方形ABCD的边长为$a$。
∵四边形ABCD是正方形,
∴$AB=BC=CD=AD=a$,$\angle ABC=\angle BCD=90^\circ$。
∵$\angle POM=45^\circ$,$\angle OCD=90^\circ$,
∴$\triangle OCD$是等腰直角三角形,
∴$OC=CD=a$。
∵$MN=10$,
∴$OM=5$,$OB=OM-BC-OC=5-a-a=5-2a$。
∵点A在⊙O上,
∴$OA=OM=5$。
在$Rt\triangle ABO$中,$AB^2+OB^2=OA^2$,
即$a^2+(5-2a)^2=5^2$,
整理得$5a^2-20a=0$,解得$a=0$(舍去)或$a=4$。
$\sqrt{5}$
∵四边形ABCD是正方形,
∴$AB=BC=CD=AD=a$,$\angle ABC=\angle BCD=90^\circ$。
∵$\angle POM=45^\circ$,$\angle OCD=90^\circ$,
∴$\triangle OCD$是等腰直角三角形,
∴$OC=CD=a$。
∵$MN=10$,
∴$OM=5$,$OB=OM-BC-OC=5-a-a=5-2a$。
∵点A在⊙O上,
∴$OA=OM=5$。
在$Rt\triangle ABO$中,$AB^2+OB^2=OA^2$,
即$a^2+(5-2a)^2=5^2$,
整理得$5a^2-20a=0$,解得$a=0$(舍去)或$a=4$。
$\sqrt{5}$
例1 如图 2.2.1,在$\odot O$中,$\widehat {AB}= \widehat {AC},∠ACB= 60^{\circ }.∠AOB= ∠BOC= ∠AOC$吗?为什么?


答案:
解:∵$\overgroup{AB}=\overgroup{AC}$
∴AB=AC
∵∠ACB=60°
∴△ABC为等边三角形
∴AB=BC=AC
∴∠AOB=∠BOC=∠AOC
解:∵$\overgroup{AB}=\overgroup{AC}$
∴AB=AC
∵∠ACB=60°
∴△ABC为等边三角形
∴AB=BC=AC
∴∠AOB=∠BOC=∠AOC
解析:
∠AOB=∠BOC=∠AOC。
理由:
∵$\widehat{AB}=\widehat{AC}$,
∴AB=AC,
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∴$\widehat{AB}=\widehat{BC}=\widehat{AC}$,
∴∠AOB=∠BOC=∠AOC。
理由:
∵$\widehat{AB}=\widehat{AC}$,
∴AB=AC,
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∴$\widehat{AB}=\widehat{BC}=\widehat{AC}$,
∴∠AOB=∠BOC=∠AOC。