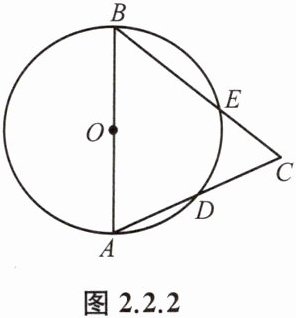
例2 如图 2.2.2,AB 是$\odot O$的直径,$AB= BC,∠C= 60^{\circ },\odot O$交 AC 于点D,交 BC 于点 E.求$\widehat {BE}$、$\widehat {AD}$的度数.

答案:
解:连接OE,OD
∵∠C=62°,AB=BC
∴∠A=∠C=62°,∠B=180°-62°-62°=56°
∵OB=OE
∴∠OEB=∠B=56°
∴∠BOE=180°-56°-56°=68°,即$\overgroup{BE}$的度数为68°
∵∠A=62°,OA=OD
∴∠ODA=∠A=62°
∴∠AOD=180°-62°-62°=56°,即$\overgroup{AD}$的度数为56°
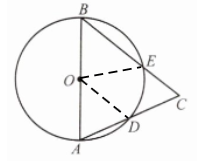
解:连接OE,OD
∵∠C=62°,AB=BC
∴∠A=∠C=62°,∠B=180°-62°-62°=56°
∵OB=OE
∴∠OEB=∠B=56°
∴∠BOE=180°-56°-56°=68°,即$\overgroup{BE}$的度数为68°
∵∠A=62°,OA=OD
∴∠ODA=∠A=62°
∴∠AOD=180°-62°-62°=56°,即$\overgroup{AD}$的度数为56°

解析:
连接OE、OD。
∵AB=BC,∠C=60°,
∴△ABC是等边三角形,∠BAC=∠ABC=60°,AB=AC=BC。
∵AB是⊙O的直径,
∴OA=OB=OE=OD。
∵OA=OD,∠BAC=60°,
∴△AOD是等边三角形,∠AOD=60°,
∴$\widehat{AD}$的度数为60°。
∵OB=OE,
∴∠OBE=∠OEB=60°,
∴∠BOE=180°-60°-60°=60°,
∴$\widehat{BE}$的度数为60°。
1
∵AB=BC,∠C=60°,
∴△ABC是等边三角形,∠BAC=∠ABC=60°,AB=AC=BC。
∵AB是⊙O的直径,
∴OA=OB=OE=OD。
∵OA=OD,∠BAC=60°,
∴△AOD是等边三角形,∠AOD=60°,
∴$\widehat{AD}$的度数为60°。
∵OB=OE,
∴∠OBE=∠OEB=60°,
∴∠BOE=180°-60°-60°=60°,
∴$\widehat{BE}$的度数为60°。
1
1. 下列结论中,正确的是(
A.相等的弦所对的圆心角相等
B.相等的弧所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的弦所对的弧相等
B
)A.相等的弦所对的圆心角相等
B.相等的弧所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的弦所对的弧相等
答案:B
2. 已知弦 AB 把圆周分成$1:5$两部分,则$\widehat {AB}$所对的圆心角的度数是(
A.$30^{\circ }$
B.$30^{\circ }或150^{\circ }$
C.$60^{\circ }$
D.$60^{\circ }或300^{\circ }$
C
)A.$30^{\circ }$
B.$30^{\circ }或150^{\circ }$
C.$60^{\circ }$
D.$60^{\circ }或300^{\circ }$
答案:C
解析:
因为弦AB把圆周分成1:5两部分,整个圆周的度数为$360^{\circ}$,所以$\widehat{AB}$所对的圆心角的度数为$\frac{1}{1 + 5} × 360^{\circ} = 60^{\circ}$。
C.
C.
3. 在$\odot O$中,如果$\widehat {AB}= 2\widehat {CD}$,那么弦 AB 与 CD 的关系是(
A.$AB= 2CD$
B.$AB>2CD$
C.$AB<2CD$
D.无法确定
C
)A.$AB= 2CD$
B.$AB>2CD$
C.$AB<2CD$
D.无法确定
答案:C
解析:
在$\odot O$中,设$\widehat{CD} = \alpha$,则$\widehat{AB} = 2\alpha$。取$\widehat{AB}$的中点$E$,连接$AE$,$BE$,则$\widehat{AE} = \widehat{BE} = \alpha$,所以$AE = BE = CD$。在$\triangle ABE$中,根据三角形两边之和大于第三边,得$AE + BE > AB$,即$CD + CD > AB$,所以$AB < 2CD$。
C.
C.
4. 如图,在$\odot O$中,$\widehat {AB}= \widehat {AC},∠C= 75^{\circ }.∠A$的度数是______.


30°
答案:30°
解析:
∵$\widehat{AB} = \widehat{AC}$,
∴$AB = AC$,
∴$\angle B = \angle C = 75^\circ$,
∵$\angle A + \angle B + \angle C = 180^\circ$,
∴$\angle A = 180^\circ - 75^\circ - 75^\circ = 30^\circ$。
30°
5. 如图,AB、CD 是$\odot O$的直径,弦$CE// AB,\widehat {CE}的度数为40^{\circ }$,则$∠AOC$的度数是
70°
.答案:70°
解析:
连接OE,
∵$\widehat{CE}$的度数为$40^\circ$,
∴$\angle COE=40^\circ$,
∵OC=OE,
∴$\angle OCE=\frac{180^\circ - 40^\circ}{2}=70^\circ$,
∵CE//AB,
∴$\angle AOC=\angle OCE=70^\circ$。
$70^\circ$
∵$\widehat{CE}$的度数为$40^\circ$,
∴$\angle COE=40^\circ$,
∵OC=OE,
∴$\angle OCE=\frac{180^\circ - 40^\circ}{2}=70^\circ$,
∵CE//AB,
∴$\angle AOC=\angle OCE=70^\circ$。
$70^\circ$
6. 如图,五边形 OABCD 的顶点 A、B、C、D 在$\odot O$上,若$\widehat {AD}的度数为150^{\circ },$$∠A= 65^{\circ },∠D= 60^{\circ }$,则$\widehat {BC}$的度数是______
40°
.答案:40°
解析:
连接OB、OC。
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD均为等腰三角形。
∵∠A=65°,OA=AB,
∴∠AOB=180°-2×65°=50°。
∵∠D=60°,OD=CD,
∴∠COD=180°-2×60°=60°。
∵五边形OABCD顶点A、B、C、D在⊙O上,$\widehat{AD}$度数为150°,
∴∠AOD=150°。
∵∠AOD=∠AOB+∠BOC+∠COD,
∴∠BOC=∠AOD-∠AOB-∠COD=150°-50°-60°=40°。
∴$\widehat{BC}$的度数是40°。
40°
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD均为等腰三角形。
∵∠A=65°,OA=AB,
∴∠AOB=180°-2×65°=50°。
∵∠D=60°,OD=CD,
∴∠COD=180°-2×60°=60°。
∵五边形OABCD顶点A、B、C、D在⊙O上,$\widehat{AD}$度数为150°,
∴∠AOD=150°。
∵∠AOD=∠AOB+∠BOC+∠COD,
∴∠BOC=∠AOD-∠AOB-∠COD=150°-50°-60°=40°。
∴$\widehat{BC}$的度数是40°。
40°