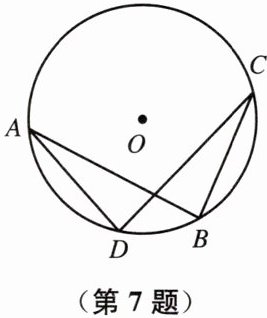
7. 如图,在$\odot O$中,弦$AB= CD$.AD 与 BC 相等吗?为什么?

答案:解:AD与BC相等,理由如下:
∵AB=CD
∴$\widehat{AB}=\widehat{CD}$
∴$\widehat{AB}-\widehat{BD}=\widehat{CD}-\widehat{BD}$
∴$\widehat{AD}=\widehat{CB}$
∴AD=BC.
∵AB=CD
∴$\widehat{AB}=\widehat{CD}$
∴$\widehat{AB}-\widehat{BD}=\widehat{CD}-\widehat{BD}$
∴$\widehat{AD}=\widehat{CB}$
∴AD=BC.
解析:
AD与BC相等。理由如下:
因为在$\odot O$中,弦$AB = CD$,所以$\overset{\frown}{AB}=\overset{\frown}{CD}$。
所以$\overset{\frown}{AB}+\overset{\frown}{BD}=\overset{\frown}{CD}+\overset{\frown}{BD}$,即$\overset{\frown}{AD}=\overset{\frown}{BC}$。
所以$AD = BC$。
因为在$\odot O$中,弦$AB = CD$,所以$\overset{\frown}{AB}=\overset{\frown}{CD}$。
所以$\overset{\frown}{AB}+\overset{\frown}{BD}=\overset{\frown}{CD}+\overset{\frown}{BD}$,即$\overset{\frown}{AD}=\overset{\frown}{BC}$。
所以$AD = BC$。
8. 如图,AB 为$\odot O$的弦,半径 OC、OD 分别交 AB 于点 E、F,且$\widehat {AC}= \widehat {DB}$.求证:$AE= BF$.


答案:相等. 提示: 分别连接 OA、OB.
解析:
证明:连接OA、OB。
∵OA、OB是⊙O的半径,
∴OA=OB,
∴∠OAB=∠OBA。
∵$\widehat{AC}=\widehat{DB}$,
∴∠AOE=∠BOF。
在△AOE和△BOF中,
$\left\{\begin{array}{l}∠OAB=∠OBA\\OA=OB\\∠AOE=∠BOF\end{array}\right.$
∴△AOE≌△BOF(ASA),
∴AE=BF。
∵OA、OB是⊙O的半径,
∴OA=OB,
∴∠OAB=∠OBA。
∵$\widehat{AC}=\widehat{DB}$,
∴∠AOE=∠BOF。
在△AOE和△BOF中,
$\left\{\begin{array}{l}∠OAB=∠OBA\\OA=OB\\∠AOE=∠BOF\end{array}\right.$
∴△AOE≌△BOF(ASA),
∴AE=BF。
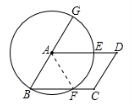
9. 如图,以$□ ABCD$的顶点 A 为圆心,AB 为半径作圆,分别交 AD、BC 于点E、F,延长 BA 交$\odot A$于点 G.
(1)求证:$\widehat {GE}= \widehat {EF};$
(2)若$\widehat {BF}的度数为50^{\circ }$,求$∠C$的度数.

(1)求证:$\widehat {GE}= \widehat {EF};$
(2)若$\widehat {BF}的度数为50^{\circ }$,求$∠C$的度数.

答案:
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠DAF,
∴$\widehat{GE}=\widehat{EF}.$
(2)因为$\widehat{BF}$的度数为50°
所以∠BAF=50°
所以∠ABF=∠AFB=65°
因为AD//BC
所以∠C=180°-∠ABF=115°.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠DAF,
∴$\widehat{GE}=\widehat{EF}.$
(2)因为$\widehat{BF}$的度数为50°
所以∠BAF=50°
所以∠ABF=∠AFB=65°
因为AD//BC
所以∠C=180°-∠ABF=115°.
